2024 ADsP 요약(3)
과목 III 데이터분석
- 데이터 마트
- 데이터 분석을 하기에 앞서 분석 목적에 맞춰 데이터를 수집, 변형하는 과정
- 데이터 웨어하우스로부터 특정 사용자가 관심을 갖는 데이터들을 주제별, 부서별로 추출하여 모든 비교적 작은 규모의 데이터 웨어하우스다.
- 효율적인 데이터 마트 개발을 위하여 R에서 제공하는 reshape, sqldf, plyr 등의 다양한 패키지를 활용할 수 있다.
- 전처리
- 데이터를 정제(cleansing)하는 과정과 분석 변수를 처리하는 과정이 포함하는 광의의 개념이다.
- 데이터 전처리 작업은 결측값과 이상값을 처리하는 ‘정제’ 작업 외에도 변수처리 작업이 포함된다. 분석 변수 처리 과정은 데이터 분석에 맞게 데이터셋의 변수 선택, 차원 축소, 파생변수 생성, 변수 변환, 클래스 불균형(불균형 데이터 처리) 등으로 이루어진다. 데이터 전처리는 ‘요리’에 빗대어 비유하자면, 본격적인 요리를 시작하기에 앞서 재료를 미리 손질하는 작업이다. 이때 요약변수와 파생변수를 생성하는 작업은 분석에 있어 매우 중요하다.
- 요약변수: 원래의 데이터로부터 기본적인 통계 자료를 추출한 변수를 의미한다. 예컨대 총 합계, 평균, 횟수, 성별 구분 등 분석에 활용되는 기본적인 변수들로 재활용성이 높다. 기초적인 통계자료들이 여기에 속한다.
- ddply( )는 데이터 프레임(d)을 입력으로 받아 데이터 프레임(d)을 내보내는 함수다. 기준이 되는 변수를 2개 이상 묶어서 사용 가능, 원하는 임의의 함수를 작성해서 사용 가능
- 파생변수: 범용으로 활용되는 기본적인 통계자료가 아닌, 특정한 목적을 갖고 조건을 만족하는 변수들을 새롭게 생성한 것을 의미한다. 예컨대 단순하게 합계를 구해 새로운 변수로 만들었다면 그것은 요약변수지만, 특정한 매장의 월별 합계 혹은 특정 기간 남성 고객의 구매 총액 등과 같이 목적 및 조건을 만족하는 변수를 생성했다면 그것은 파생변수이다. 파생변수에는 목적에 따른 특정한 의미가 부여된다. 주관적일 수 있으므로 논리적 타당성을 갖추어야 한다.
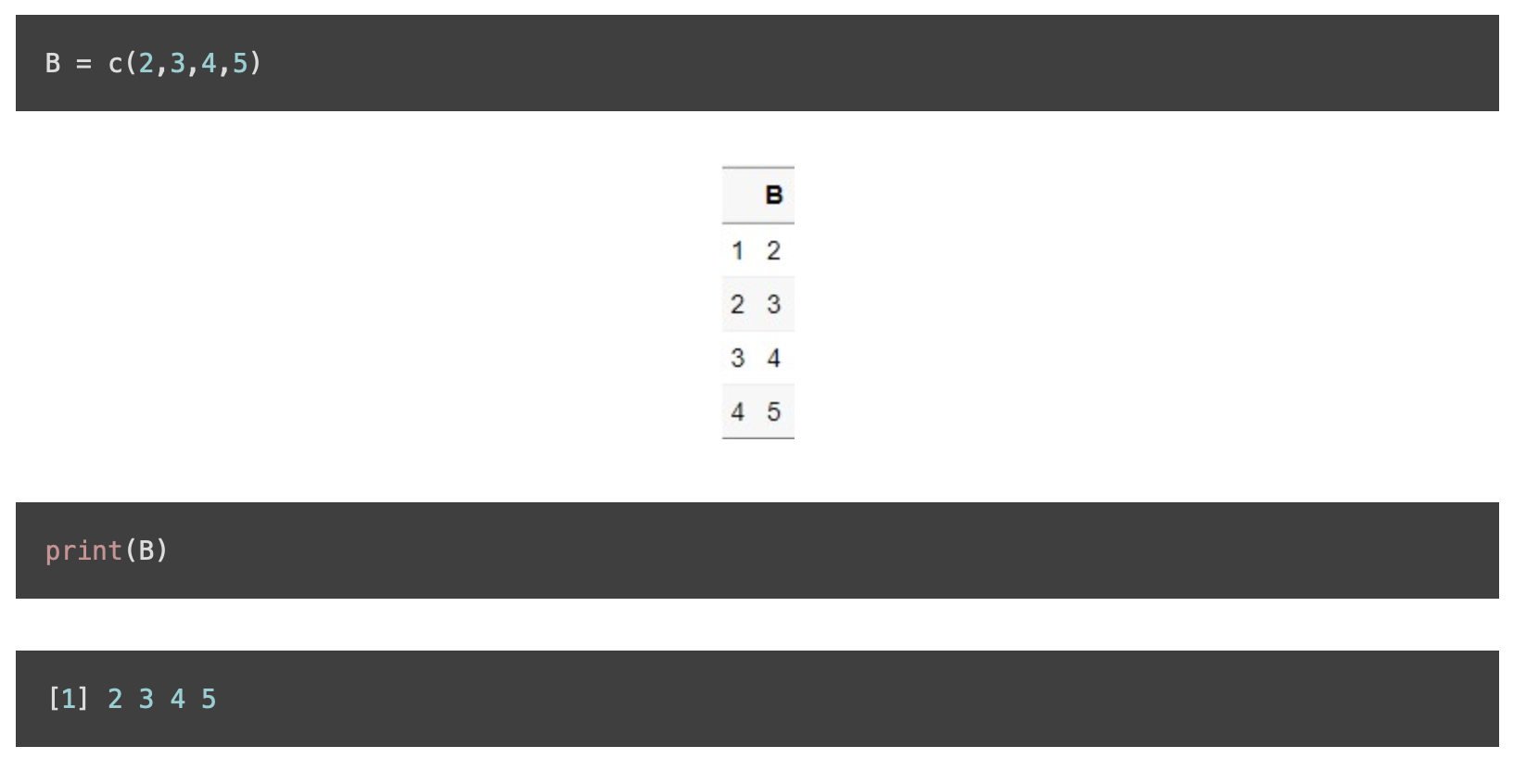
c()는 Combind의 약자를 나타내는 명령어로, R에서 매우 자주 쓰이는 명령어이다. c()는 벡터를 만드는데 사용된다. 여기서 벡터라고 하면, 데이터에서 하나의 ’열(Column)’을 의미한다. 즉, 데이터가 세로로 저장된다고 생각하면 된다.
- summarise는 데이터 요약, transform은 기존 데이터에 추가
- elapsed : R작업과 운영체제 시스템 총 작업경과 시간 - 명령문의 시작부터 종료까지
- 탐색적 분석(EDA; Exploratory Data Analysis)
- 데이터를 이해하고 의미 있는 관계를 찾아내기 위해 데이터의 통곗값과 분포 등을 시각화하고 분석하는 것으로 이를 통해 분석 모델을 구축할 수 있다.
- 결측값
- 결측값은 존재하지 않는 데이터를 의미하며, NA(Not Available)로 표현하지만 데이터를 수집하는 환경에 따라 null, 공백, -1 등 다양하게 표현될 수 있다.
- 데이터 분석에 앞서 결측값 처리는 중요한 과제 중 하나다. 결측값을 삭제하는 것이 일반적이나 경우에 따라 의미를 갖는 경우도 있다.(예: 특정 설문 문항에 대해 결측값이 많다는 것은 해당 문항의 민감함을 나타내는 측도로써 활용 가능하다.)
- 결측값 처리를 위한 대표적인 패키지로 Amelia와 DMwR2 패키지가 있다
- 결측값 대치 방법 ⭐️⭐️
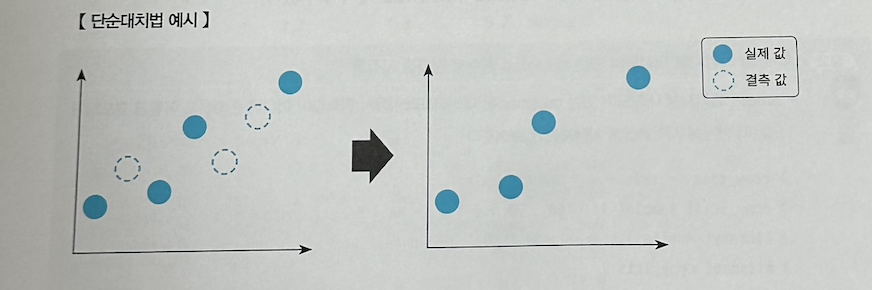
- 단순 대치법
- 결측값이 존재하는 데이터를 삭제하는 방법이다.
- 가장 쉬운 결측값 처리 방법이지만 결측값이 많은 경우 대량의 데이터 손실이 발생할 수 있다.
- 단순 대치법을 위한 함수로 complete.cases 함수가 있다. complete.cases는 하나의 열에 결측값이 존재하면 FALSE, 존재하지 않으면 TRUE를 반환한다.
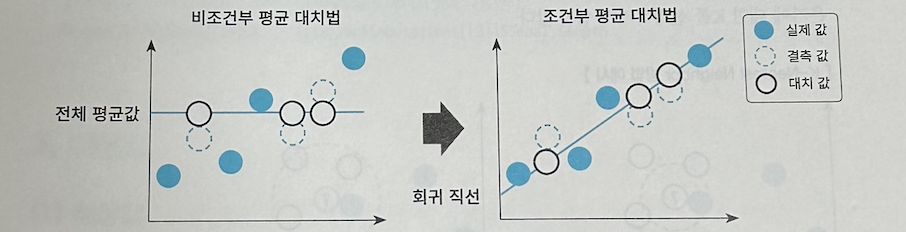
- 평균 대치법
- 관측 또는 실험으로 얻은 데이터를 대표할 수 있는 평균 혹은 중앙값으로 결측값을 대치하여 불완전 한 자료를 완전한 자료로 만드는 방법이다.
- 비조건부 평균 대치법과 조건부 평균 대치법이 있다. 비조건부 평균 대치법은 데이터의 평균값으로 결측값을 대치하는 반면 조건부 평균 대치법은 실제 값들을 분석하여 회귀분석을 활용하는 대치 방 법이다.
- 평균값 혹은 중앙값을 직접 구하여 결측값을 대치해도 되지만 DMWR2 패키지의 central Imputation 함수를 사용하여 쉽게 대치할 수 있다.
- na.rm은 결측치가 있는 다른 행에 영향을 주지 않지만, na.omit은 결측치가 있는 행 자체를 제외해버리는 차이가 있다.
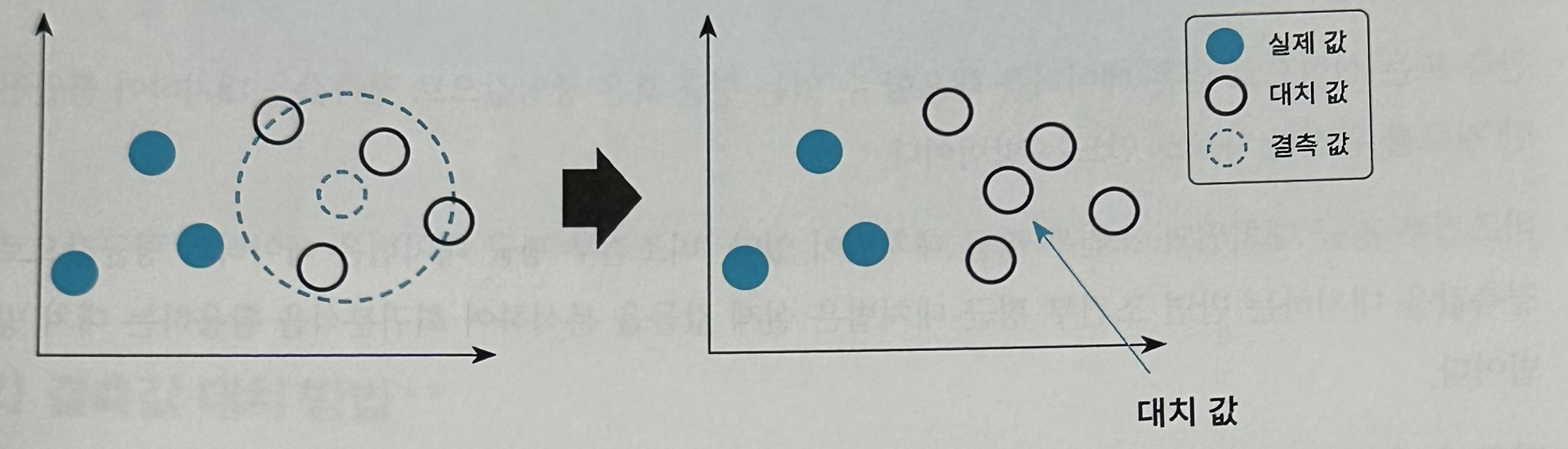
- 단순 확률 대치법
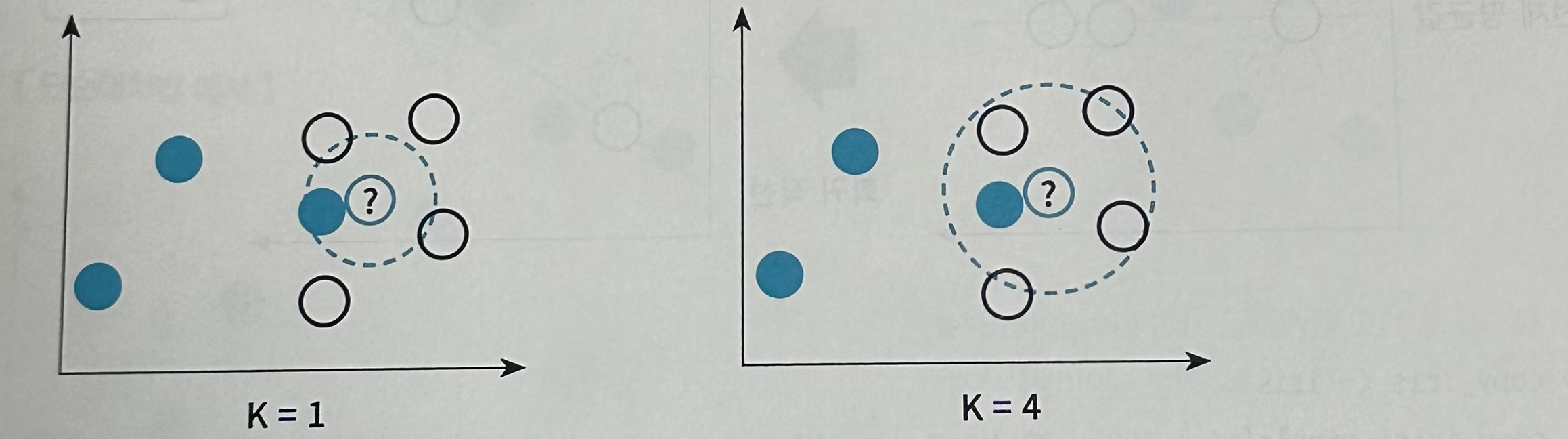
- 평균 대치법에서 추정량 표준 오차의 과소 추정 문제를 보완하고자 고안된 방법이다. 대표적인 방법으로 K-Nearest Neighbor 방법이 있다.
- K-Nearest Neighbor 방법: K 최근접 이웃 알고리즘으로 주변 K개의 데이터 중 가장 많은 데이터 로 대치하는 방법이다. 아래 그림에서 K = 1인 경우 결측값으로 파란색이 유력해 보이지만 K= 4인 경우에는 결측값으로 검정색이 유력해 보인다. 따라서 주변 몇 개의 데이터가 결측값을 대치하기 좋 은가에 대한 K를 선정하기가 쉽지 않다.
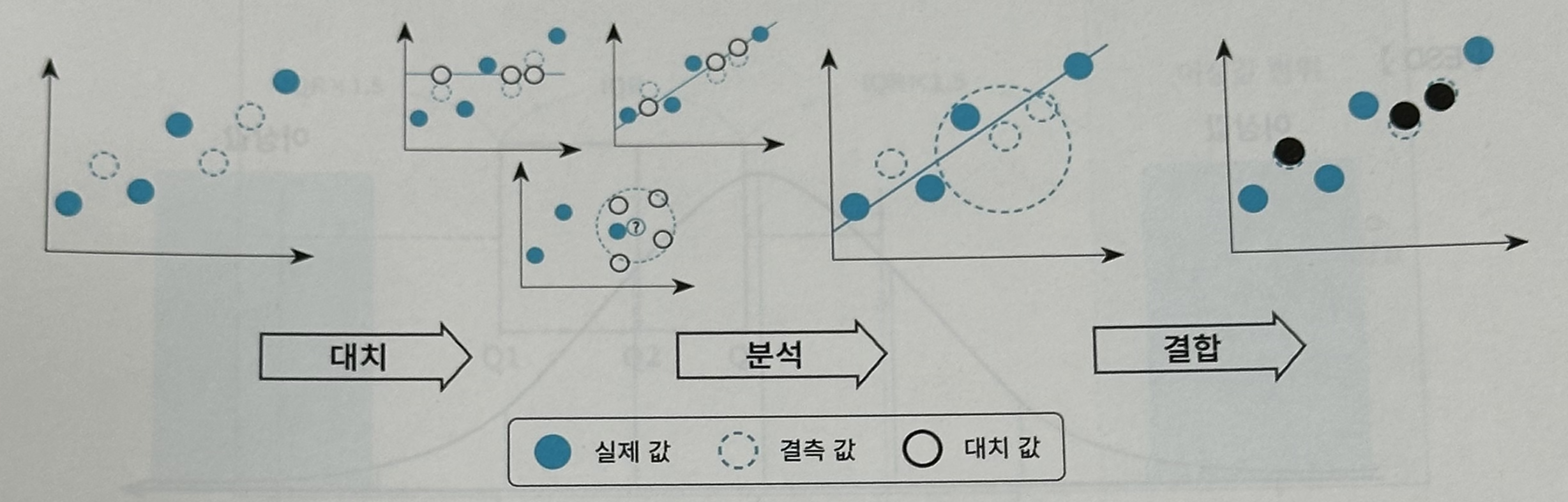
- 다중 대치법
- 여러 번의 대치를 통해 11개의 임의 완전자료를 만드는 방법으로, 결측값 대치, 분석, 결합의 세 단계 로 구성되어 있다.
1 2 3 4 5 6 7 8
# 테스트를 위한 결측값을 가진 iris 데이터 생성 > copy_iris <- iris # 원본 데이터를 유지 > copy iris[ sample( 1 : 150 , 30 ) , 1 ] 〈- NA # Sepal.Length에 30개의 결측값 생성 > library ( Amelia) > iris_imp <- amelia( copy_iris, m= 3, cs = "Species" ) # cs는 cross-sectional로 분석에 포함될 정보를 의미 # 위 amelia에서 m 값을 그대로 imputation의 데이터셋에 사용한다. > copy_iris$Sepal.Length <- iris_imp$imputations[[3]]$Sepal.Length
- 단순 대치법
- 이상값 판단 ⭐️⭐️⭐️
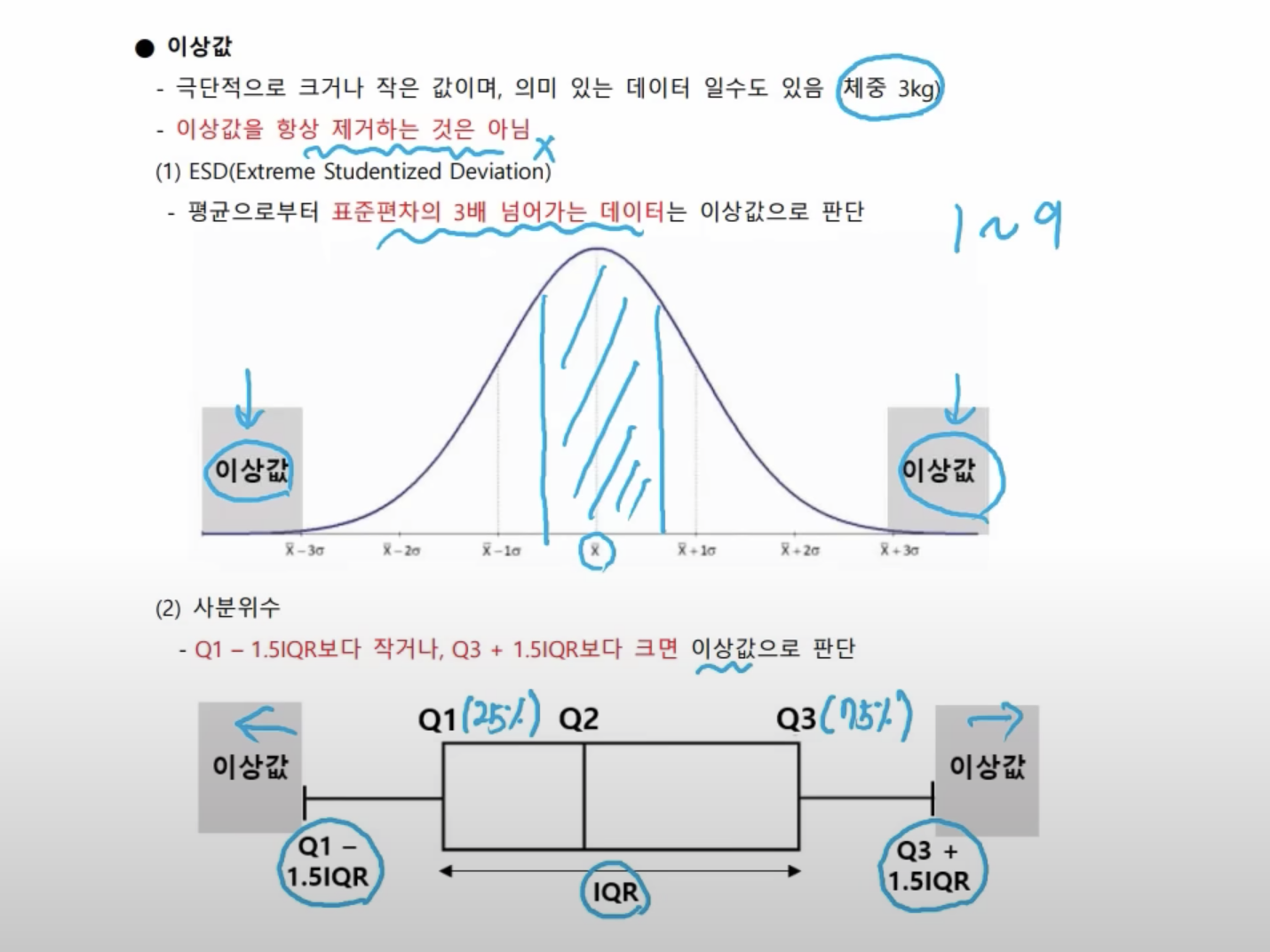
- ESD(Extreme Studentized Deviation)
- 평균으로부터 ‘표준편차 3’만큼 떨어진 값들을 이상값으로 인식하는 방법이다. 정규분포에서 99.7%의 자료들은 ‘표준편차 3’ 안에 위치하므로 전체 데이터의 약 0.3퍼센트를 이상값으로 구분한다.
- 사분위수
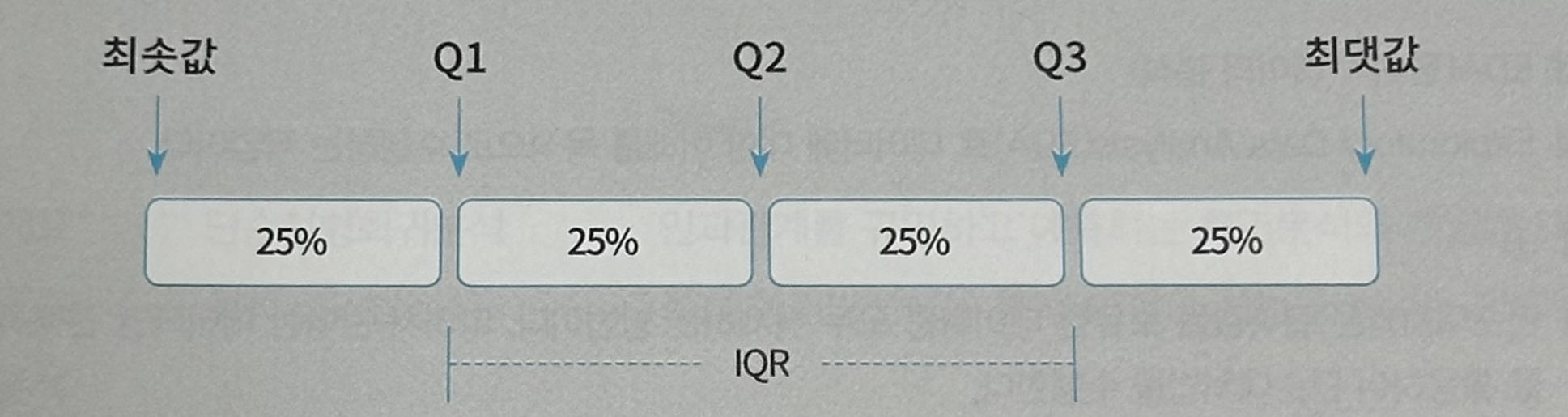
- 사분위수를 이용하여 25%에 해당하는 값(Q1)과 75%에 해당하는 값(Q3)을 활용하여 이상치를 판 단하는 방법이다. 자료를 크기 순서대로 나열했을 때 사분위수로 나눌 수 있다.
- 가장 작은 하한 사분위수를 Q1이라고 하고, 가장 큰 사분위수인 상한 사분위수는 Q3라고 한다. 여 기서 IQR이란 사분위의 정상 범위인 Q1과 Q3 사이를 의미하며, 사분범위(Interquartile Range, IQR)라고 한다.
- 일반적으로 사분범위에서 1.5분위수를 벗어나는 경우 이상치로 판단한다. 다시 말해 Q1 - 1.5 x IQR(하한 최솟값)보다 작거나 Q3 + 1.5 x IQR(상한 최댓값)보다 큰 값은 이상값으로 간주한다.
- 시각적으로 상자 그림의 아웃라이어에 위치해 점으로 표현된 데이터를 이상값으로 판단할 수 있다.
- 사분위수는 측정값을 최솟값에서 최댓값까지 오름차순으로 정렬한 자료를 4등분했을 때 각 등분 위치에 해당 하는 값을 의미한다. IQR은 1분위 수(Q1)부터 3분위 수(Q3)까지의 범위를 의미하며. 2분위 수(Q2)는 앞서 자주 언급한 중앙값(median)이다.
- ESD(Extreme Studentized Deviation)
- 기하 분포
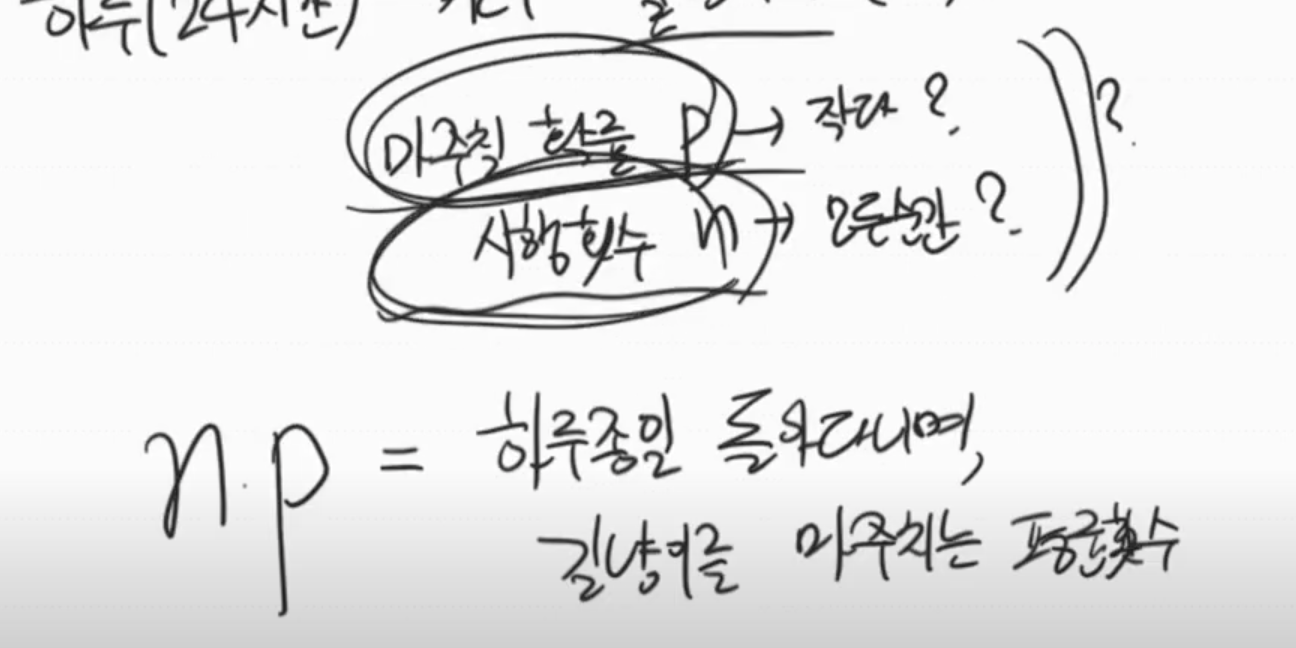
- 포아송 분포는 시행횟수 n이 무수히 커지고, 발생 확률 p가 무수히 작아질 때 유도되는 분포
n*p는 이항분포의 평균이다. 포아송 분포에서는 n과 p를 각각 다루지 않고, 람다를 사용한다.
- 95%까지 허용하는 것이 일반적이다. 95%를 벗어나면 기각역이다.
- 유의수준을 보통 5%로 가정한다. 나의 주장이 틀릴 확률이 3%일 경우, 너의 말이 맞다. ⇒ 귀무가설 기각
- alternative hypothesis: 대립가설
- 신뢰수준 95%, 귀무가설의 기각 혹은 채택은 p-value(틀릴 확률)와 유의수준(허용, 5%)을 보면 된다. 두 학교의 성적이 같지 않다는 내 주장이 55%나 틀릴 확률이다. 너의 말은 틀렸다. ⇒ 귀무가설 채택
- 서로 다른 모집단에 대한 평균비교 검정이므로 독립 표본
- 검정 시 표본으로 모집단의 특성을 파악하는 게 목표(정규 분포나 t분포를 그린다는 가정하에 검증을 수행)
- 비모수 검정은 모집단에 대한 아무런 정보가 없을 때
- 회귀분석
- 일차함수(x로 y를 결정함) → x는 독립변수, y는 종속변수
- x, y로 회귀분석을 결정했을 때, 계산값과 예측값의 차이가 존재하는데, 이를 잔차라 부른다. 오차와 비슷한 개념이나, 오차는 모집단에서 사용한다.
- 우리는 표본에서의 데이터를 가지고 회귀 분석을 수행하므로, 잔차라고 한다.
- w와 b값이 결정되어야 x에 값을 집어넣었을 때 y값이 결정된다. w를 회귀계수 또는 가중치라고 하며, b를 절편이라 한다. 잔차의 제곱합이 최소가 되도록 구한다.
- ①, ②는 계산값과 예측값의 차이가 크나(잔차가 큼) ③은 잔차가 작다. ③이 되는 식을 구해야 하는데, 이때 사용하는 방법이 최소제곱법이다.
- R-squared: 최소제곱법을 통해 w와 b값을 알아내면, 해당 모델(회귀식)이 좋은 모델인지 판정한다. 이 값은 0~1 사이의 값(0은 좋지 않음, 1은 좋음)
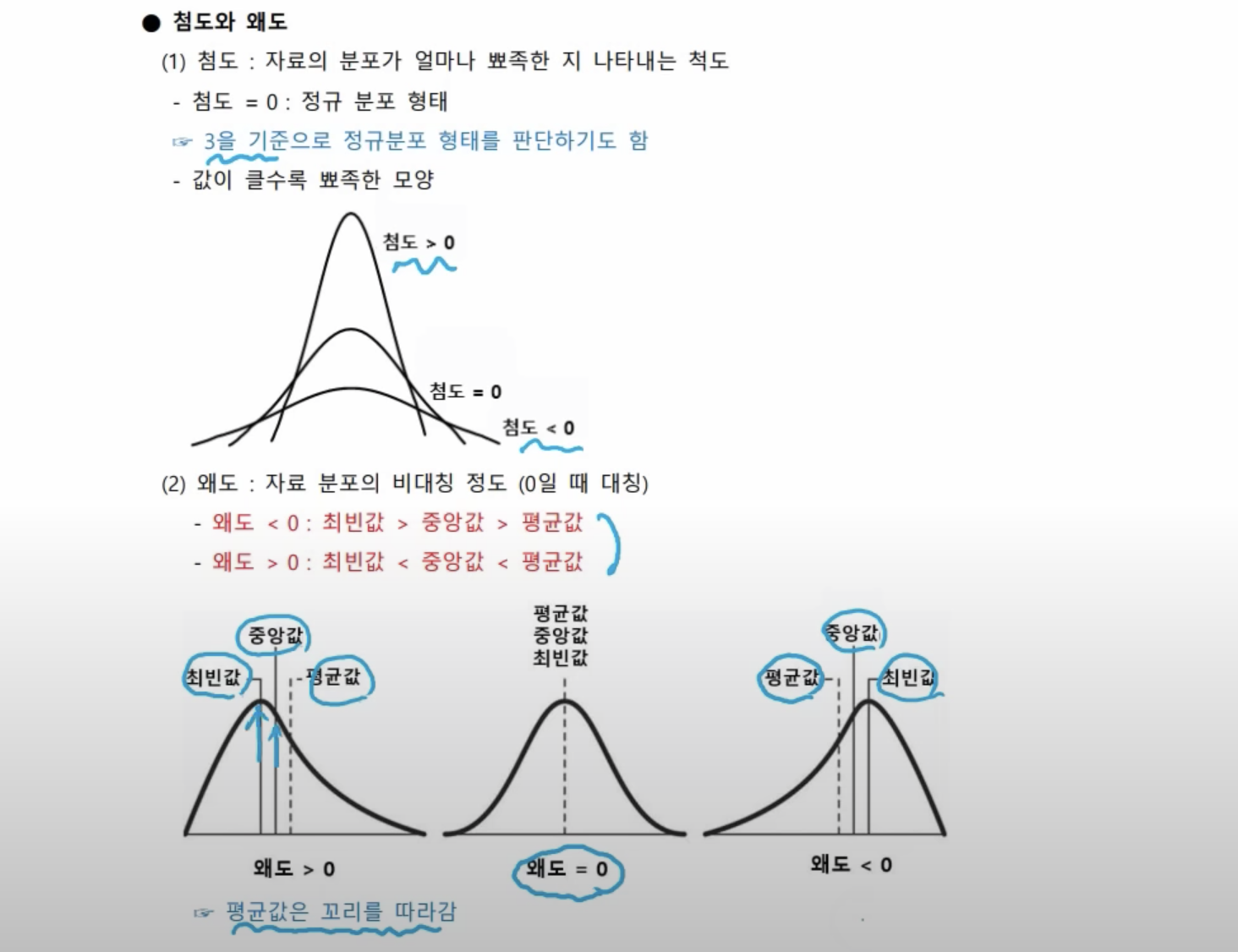
- 회귀분석의 가정 - 내용과 연결 ⭐️⭐️⭐️
- 정규성은 정규 분포를 그리느냐?
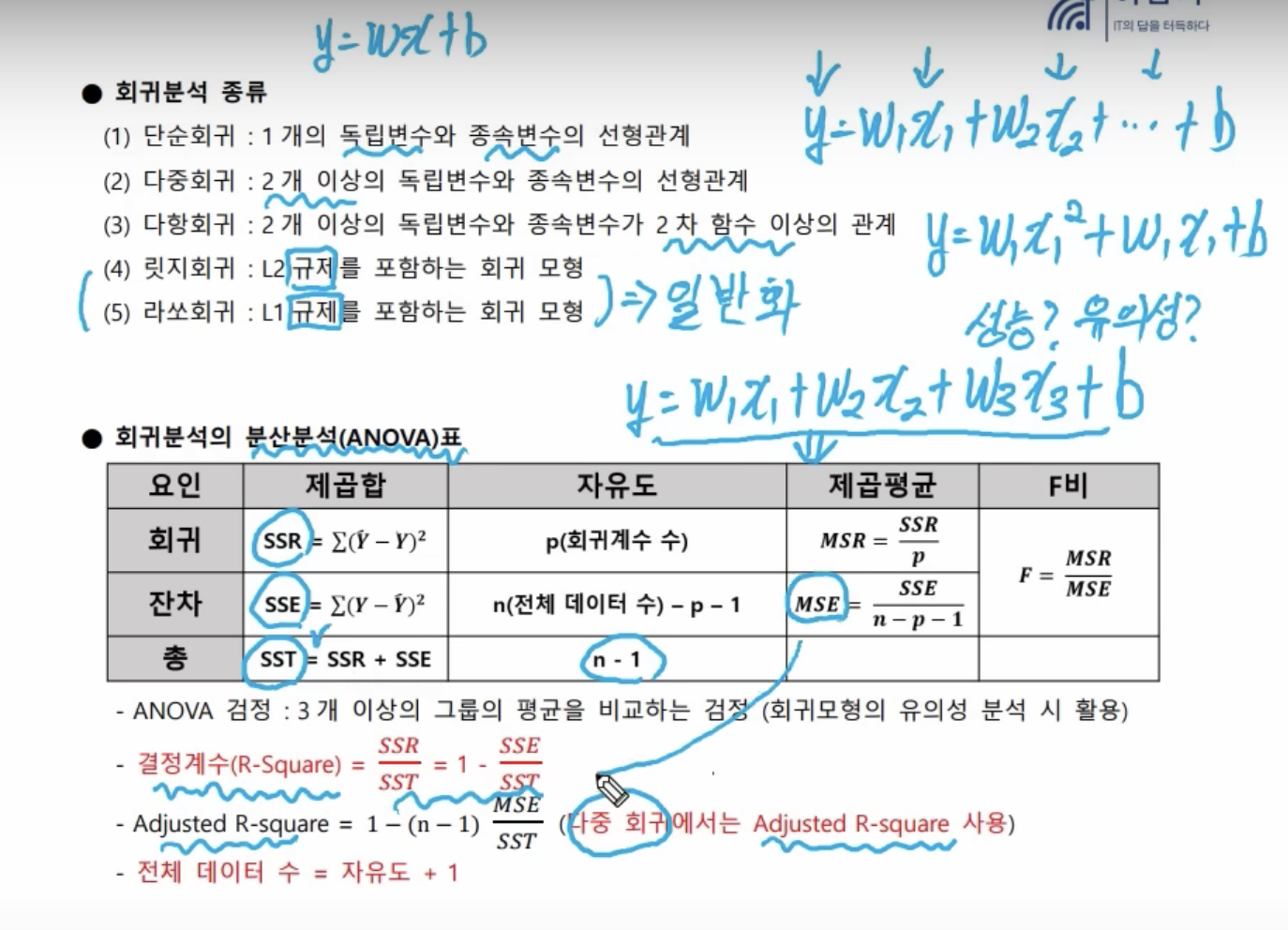
- 회귀분석 종류
- 다중회귀: 여러가지 독립변수들이 모여서, 종속변수를 결정한다.
- 다항회귀: 일상생활 분석시 위와 같은 선형관계만이 존재하진 않을 것, 2차 함수 이상의 관계
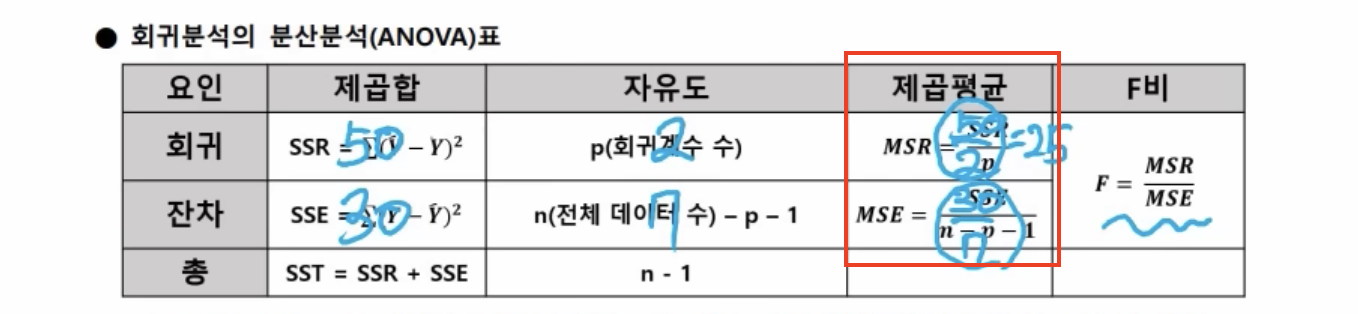
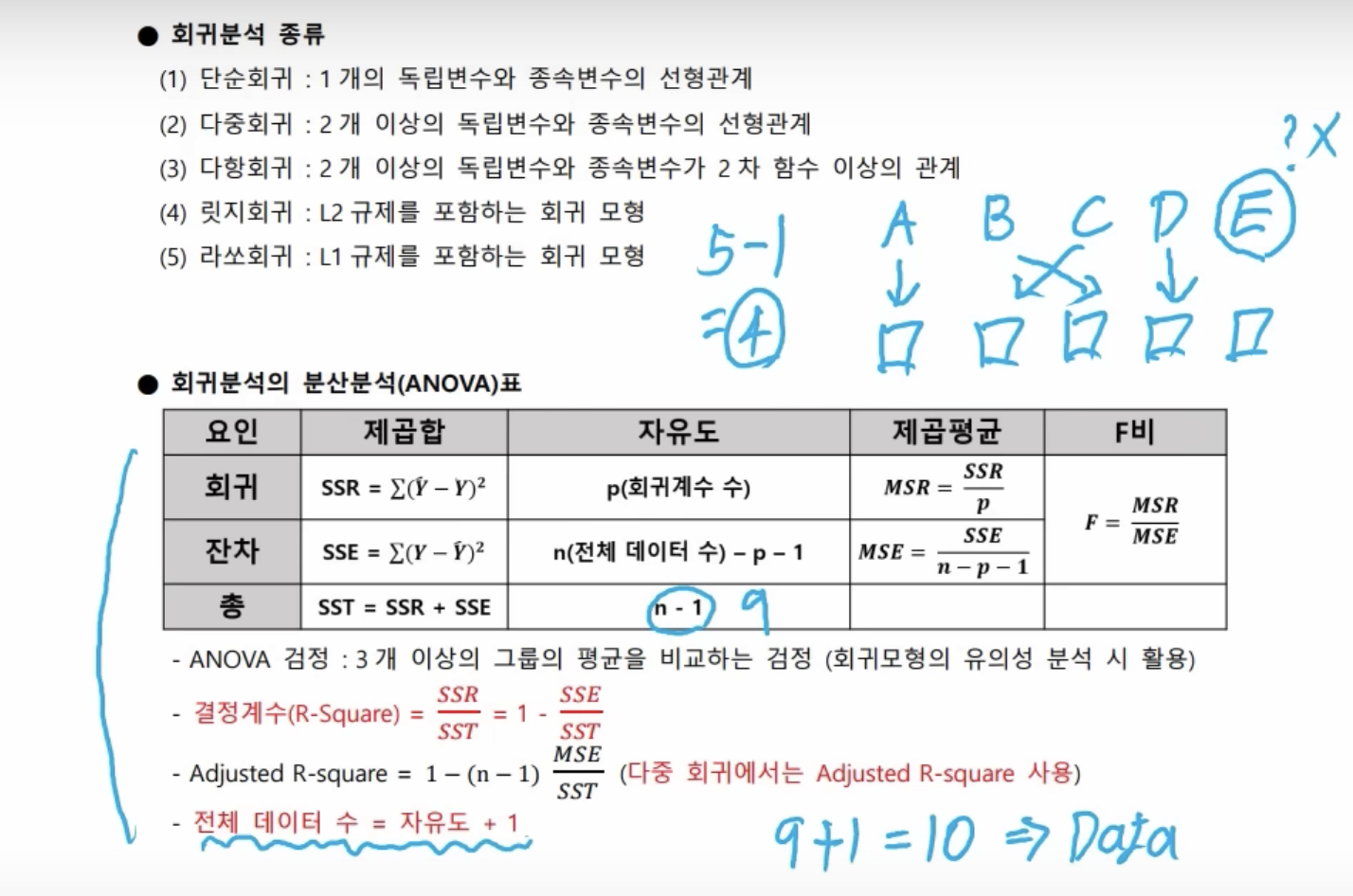
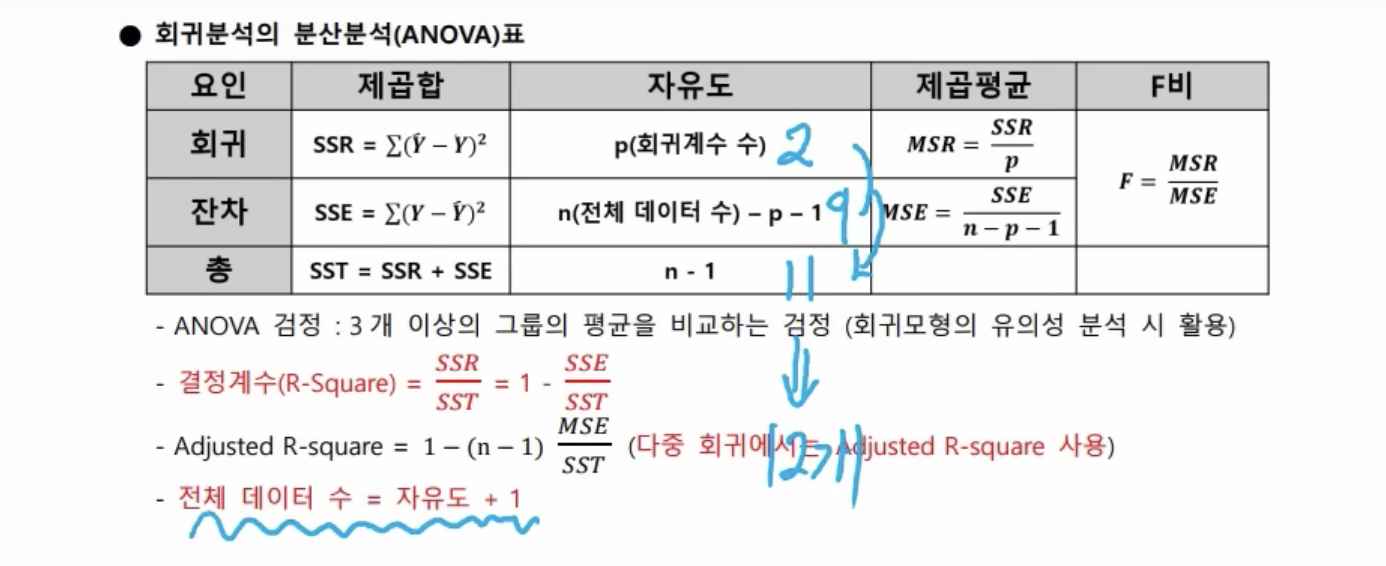
- 회귀분석 분산분석(ANOVA)표
- 회귀분석 후 ANOVA(분산분석)표를 작성하게 된다.
- 다중회귀는 수정된 R-squared 값을 사용한다.
- 자유도가 9일 경우, 10개의 데이터로 분석했음을 알 수 있다. 그림에서 E는 자유도가 없으므로 자유도는 5-1 = 4가 되는 것이고, 전체 데이터는 1을 더한 5가 된다.
- 회귀모형의 검정 - 순서를 통해 문제 풀이
- 독립변수와 종속변수를 설정하면, 회귀계수 값을 추정하게 된다. 이 모형(회귀식) 자체가 통계적으로 유의미한지 결정할 때는 F검정을 수행한다.
- 회귀계수가 0이면 제대로 된 모델이 아니므로 귀무가설은 기각을 하는 게 목적이다. 귀무가설이 0이 아닐 경우, 각각의 회귀계수가 0인지에 대하여 t검정을 수행한다.
- 두 가지 귀무가설이 기각되면, 해당 모델(회귀식)을 활용할 수 있다.
- 이 모델이 설명력을 갖는가에 대해서는 R square 값으로 결정한다.
- 신뢰도가 주어져있지 않으면 무조건 95%라고 생각하기(가장 일반적) → 유의확률은 0.05가 된다.
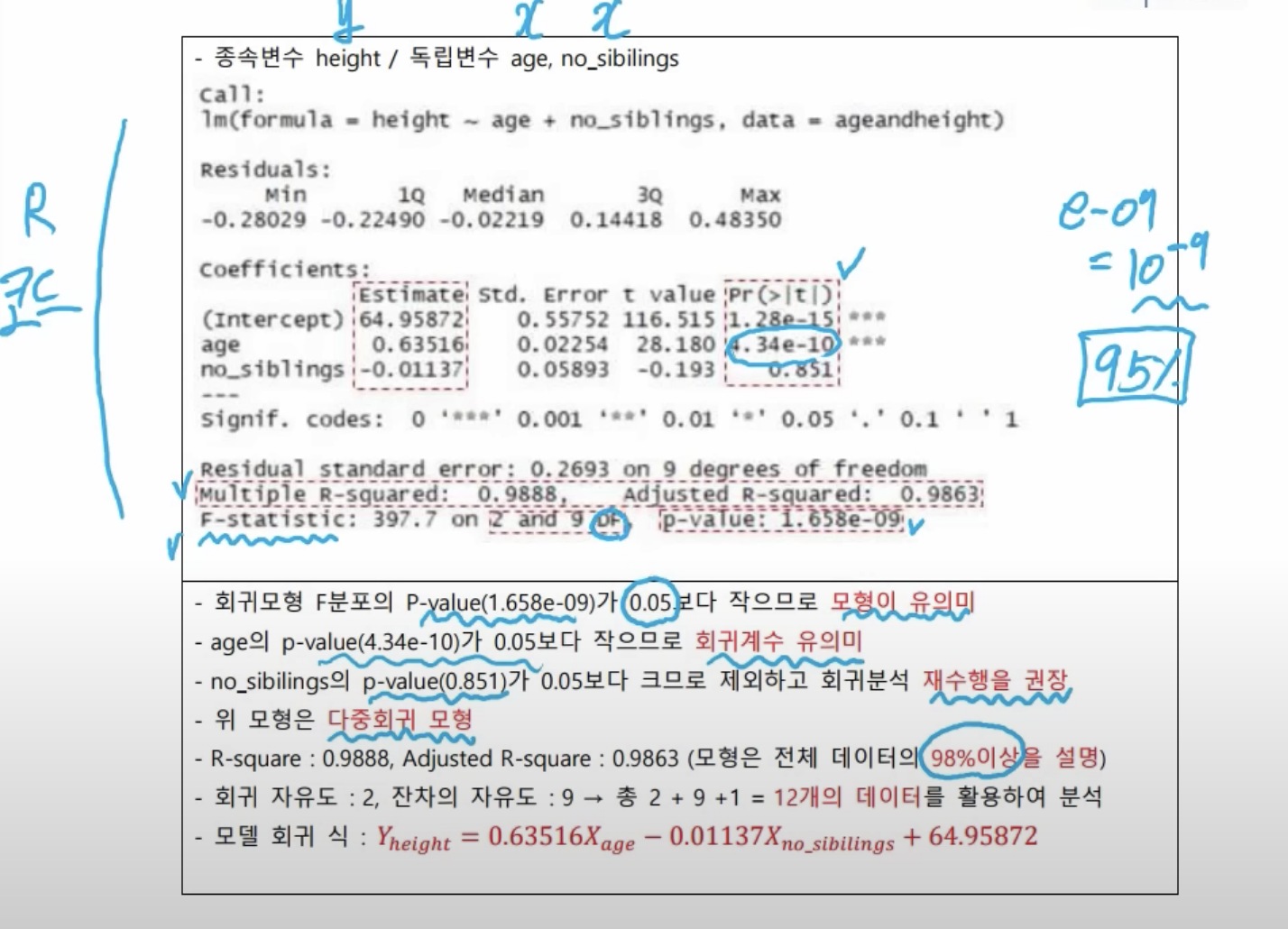
- F검정의 p-value 값이 엄청 작은 값 = 나의 주장이 틀릴 값일 확률이 너무도 작음 → 너의 말이 맞음, 귀무가설(모든 회귀계수는 0이다.) 기각 ⇒ 이 모형(회귀식)은 유의미함
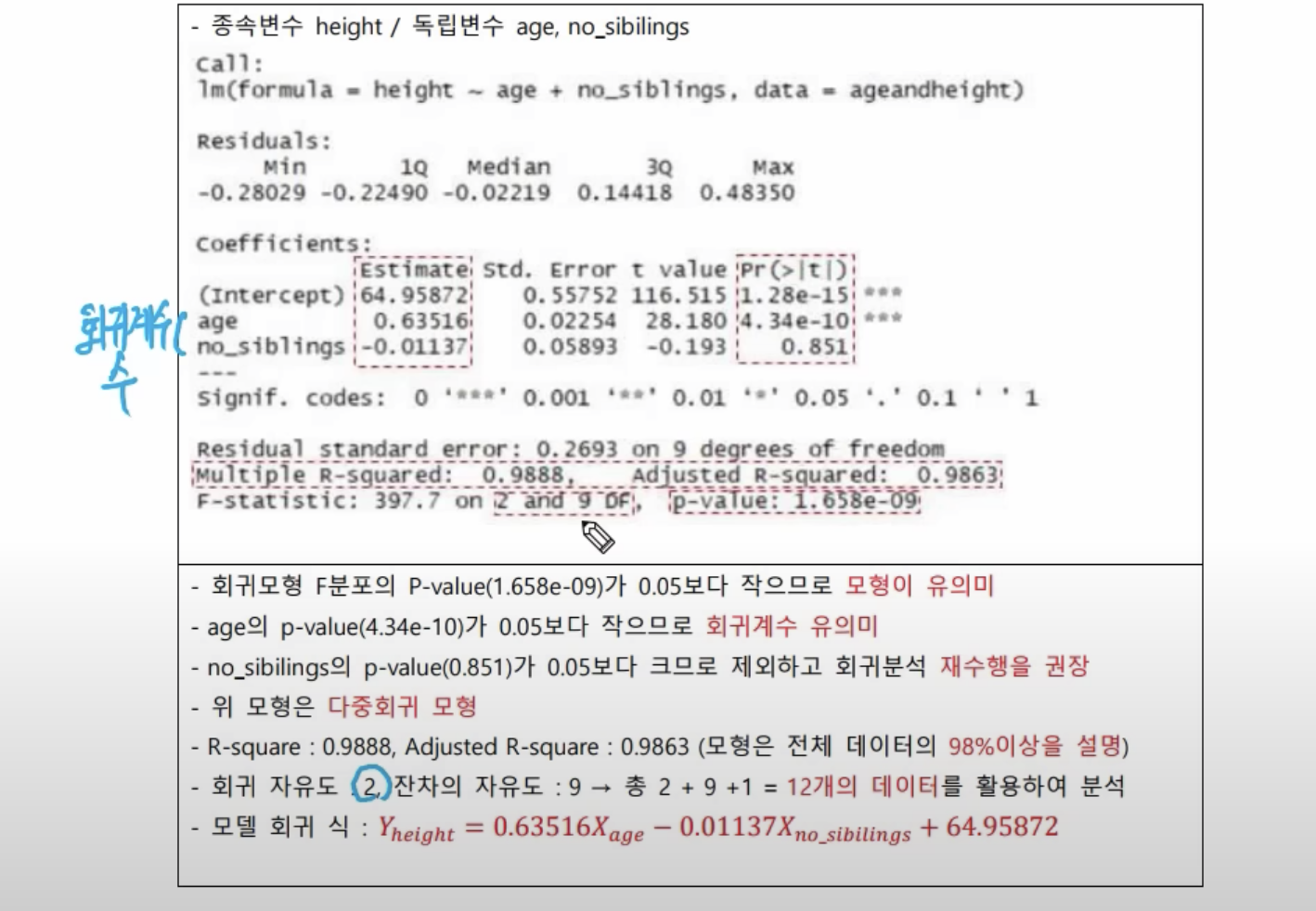
- 각각의 회귀계수에 대해 t검정 수행
- age 독립변수의 경우, p-value가 0.05보다 작으므로, 회귀계수가 유의미함(귀무가설 기각)
- no_siblings 독립변수의 경우, p-value(85%)가 0.05보다 큼 → 너의 말이 틀림, 귀무가설이 맞음(이 회귀계수는 0이다.) ⇒ 회귀분석 재수행 권장(무조건 재수행은 x)
- 재수행을 수행하진 않았지만, 독립변수가 2개이므로 다중회귀 모형이 된다.
- 설명력을 보기 위해서 R squared를 봄 - 0.9888과 추정치 0.9863 ⇒ 이 모형은 전체 데이터의 98% 이상을 설명한다고 말할 수 있다.
- 자유도(DF; degree of freedom)
- 회귀 자유도 = 회귀계수의 수
- 회귀식
- 회귀계수는 Estimate에서 알 수 있다.
- Intercept는 절편에 해당한다.
- 전진선택법: 독립변수를 하나씩 추가하면서 유의성을 판정한다.
- 다변량 분석
- 상관분석
- 독립변수가 여러 개 있는 다변량, 즉, 다중회귀에서 x1은 y를 결정할 수 있어야하며 x2도 y를 결정할 수 있어야 좋은 모델이다.
- 선형적 관계가 존재하면 안 된다.(= 독립변수들끼리 불안정하면 안 된다.) 선형적 관계가 존재하는 지 파악하는 것이 상관분석이다.
- 다중공선성: 다중회귀분석에서 설명변수들 사이에 상관관계가 클 때 모델이 불안정해진다.
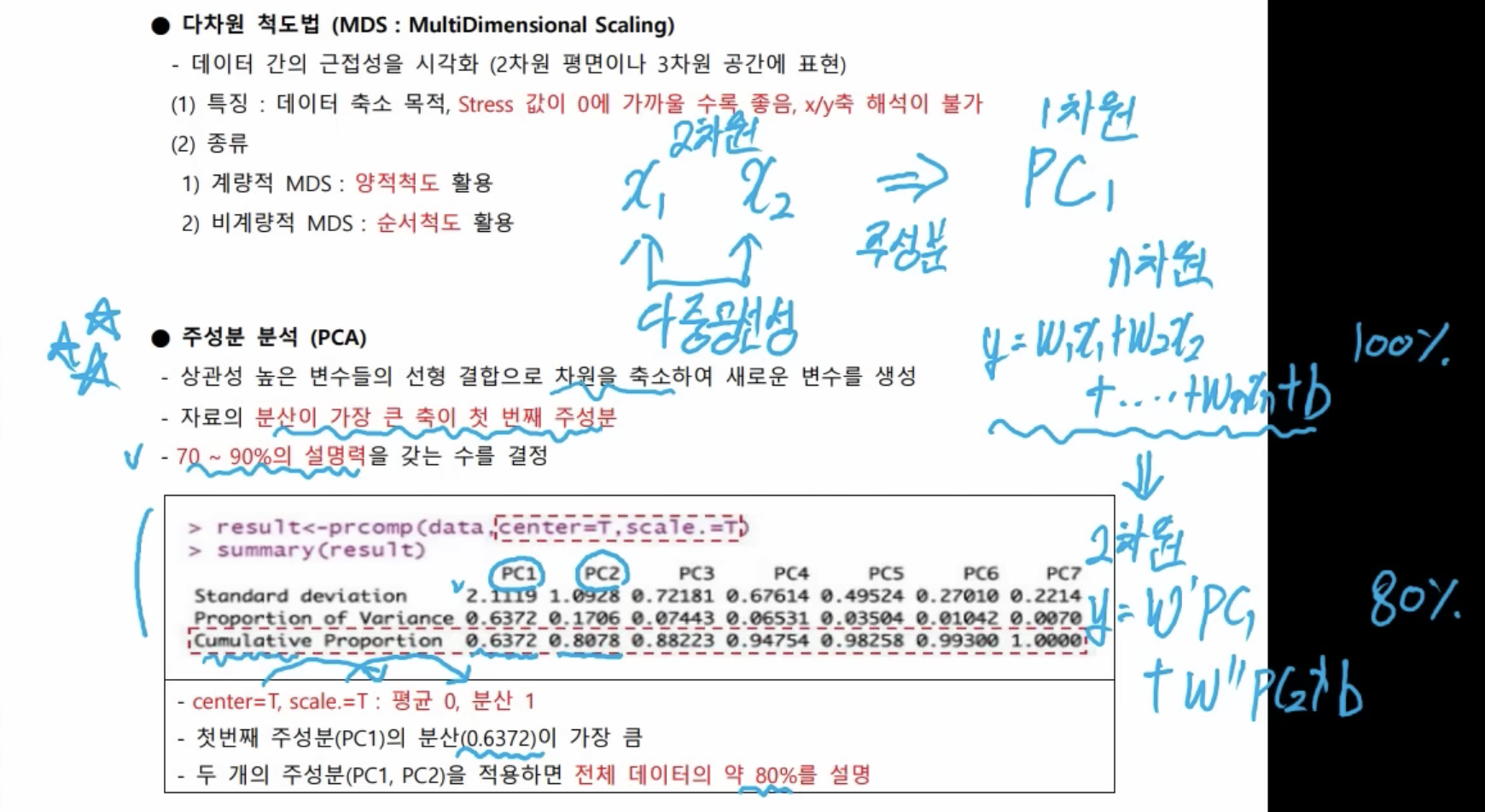
- 다차원 척도법
- x1과 x2의 관계를 시각화 시킨다. 눈으로 보면 상관관계 유무를 파악하기 쉽다.
- 주성분 분석(PCA)
- 다중공선성 문제 → 둘을 합쳐 하나의 새로운 변수로 생성
- 하나의 차원으로 줄이면(PC1), 설명력이 0.6372가 되고, 분산이 가장 크다.
- 두 번째 주성분까지 선택하면(PC1, PC2), 설명력이 누적되면서 전체 데이터의 약 80%(0.8078)를 설명한다.
- 독립변수가 n개면 n차원, n차원을 2차원으로 축소한 회귀식으로 변경했을 때, 본래가 100%라고 했을 때, 주성분 분석을 통해 차원을 축소했을 때는 80%를 설명할 수 있다.
- 상관분석
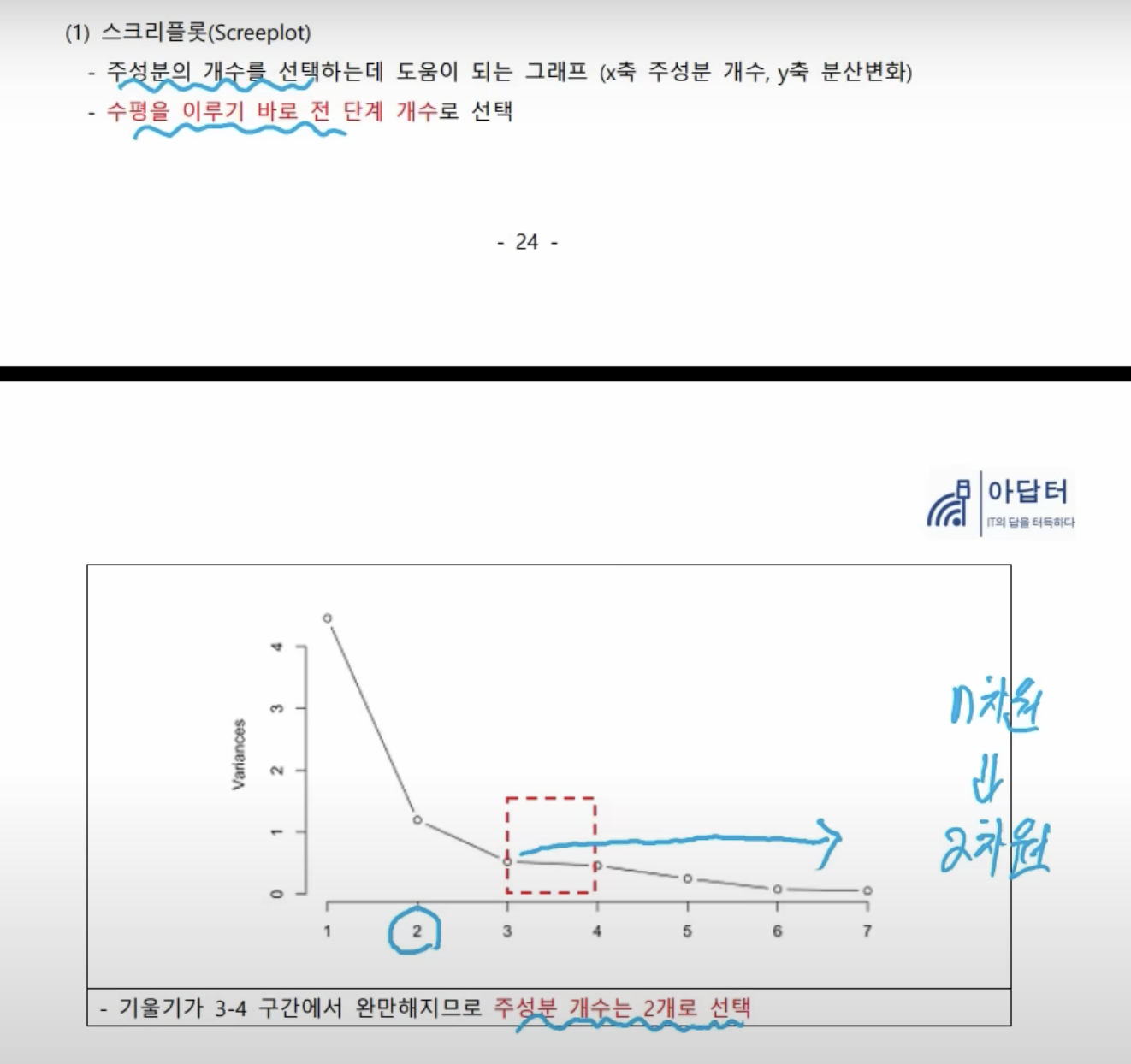
- 분산이 평행해진다 = 설명력이 높지 않다. → 수평을 이루기 바로 전 단계 개수로 선택
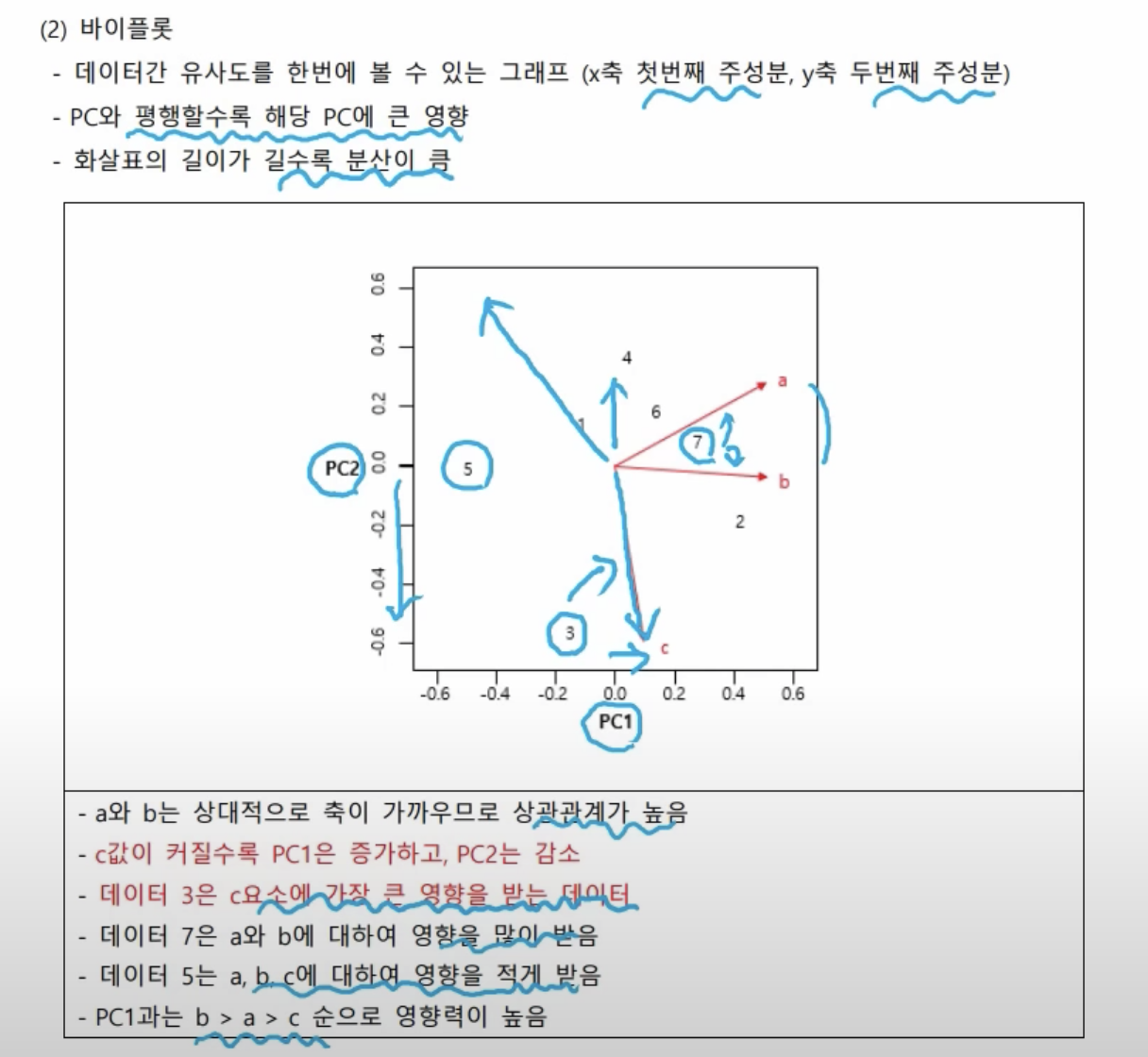
- 데이터 3은 c와 가장 가까이 있으므로, c요소에 가장 큰 영향을 받는 데이터
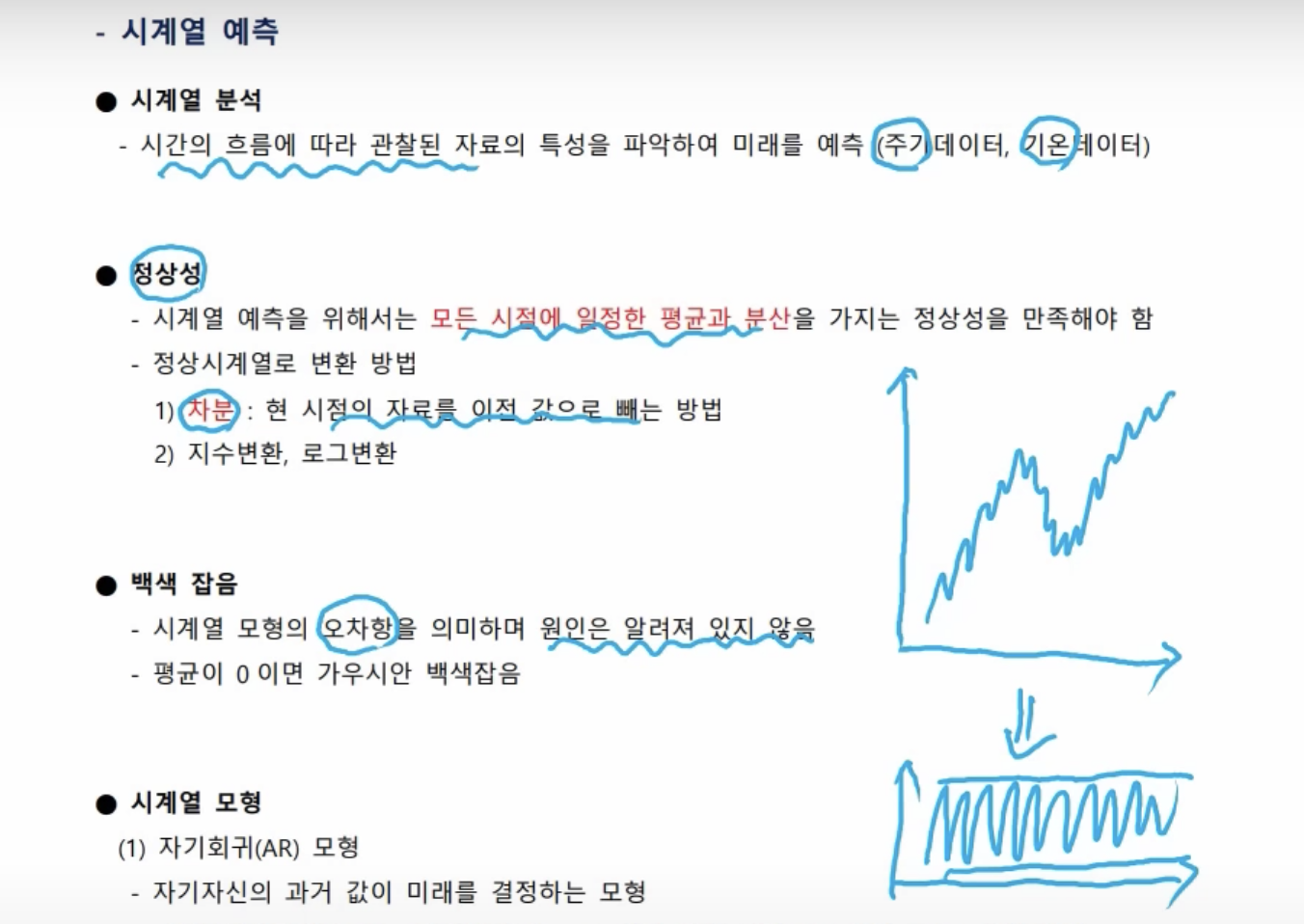
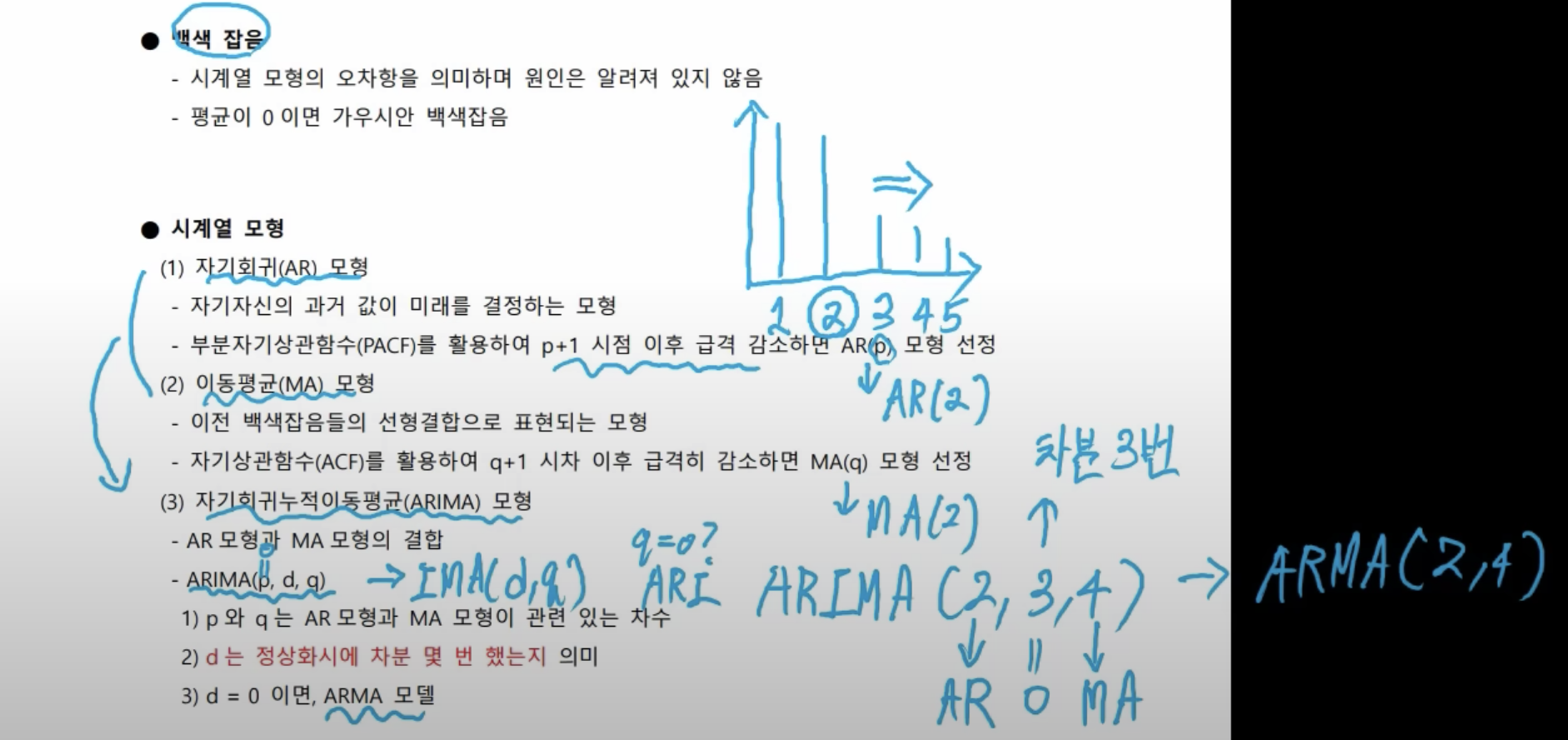
- 시계열 분석에서 오차를 백색 잡음이라 표현한다.
- 시계열 모형은 세 가지가 있다. AR 모형, MA 모형, ARIMA(아리마) 모형이 있다.
- AR(자기 회귀) 모형은 자기 자신의 과거 값이 미래를 결정한다. 그래서 부분 자기 상관 함수로 활용해서 p+ 1시점 이후 급격히 감소하면 AR(p) 모형을 선정한다.
- MA이동 평균) 모형은 백색잡음들의 선형 결합으로 표현되는 모형이다. 이건 자기 상관 함수를 사용해서 q+ 1 시점 이후 급격히 감소하면 MA(q) 모형을 선정한다,
- 부분 자기 상관나 함수 자기 상관 함수 상관 함수를 써서 1일 전, 2일 전, 3일 전, 4일 전, 5일 전 있으면 이때 1일 전이 오늘과는 상관이 크고, 2일 전도 오늘과 상관이 큰데 3일 전부터 상관이 낮으면 모델을 선정할 때 3일 전까지는 우리가 고려할 필요가 없다는 것이다.
- 즉, 플러스 1시점이 급격히 감소하면 급격히 감소하기 이전 시점인 이틀 전까지만 모델에 활용을 하자는 것이다.
- 부분 자기 상관 함수의 AR(2) 모델이 되는 것이고, 자기 상관 함수는 MA(2) 모델이 되는 것이다. 그리고 이 두 개를 결합해서 더 좋은 모델을 만들어 보자 하는 것이 바로 아리마 모델이다.
- AR, MA 모델의 결합인데 아리마 pdq로 표현을 한다. p와 q는 AR과 MA에서 왔다. d는 정상화 시에 차분을 몇 번 했는지를 의미한다.
- 차분은 가운데값 고르면 된다. d가 0이면 (ARMA)알마 모델이라고 얘기를 한다. 즉, 알마 2라고 이야기 한다.
- p가 0인 경우, AR이 없어진 것이므로 IMA dq 모델이 되는 것이고, q가 0이면 ARI 모델이 되는 것이다.
- 데이터를 분할해서 학습하기도 한다.
- 과대적합과 과소적합
- 과대적합: 매우 복잡해진 모델을 단순화하기 위해 회귀에서 릿지나 라쏘를 규제한다.
- 분할된 데이터 셋 종류
- 50%는 공부, 30%는 나 자신을 평가하는 자가진단 후, 부족한 부분을 다시 학습(50%) - 왔다갔다 함 → 시험 전 날 자체 모의고사(안 푼 문제)로 모델을 평가한다.(20%)
- 절대적이진 않지만, 일반적인 수치
- 분할된 데이터의 학습 및 검증 방법
- k-fold 교차검증: 돌아가면서 나머지로 학습하고, 1개로 평가
- LOOCV(Leave-One-Out Cross-Validation)10개씩 평가하는 것은 데이터 수가 아까우므로, 1개의 데이터로만 평가하고 나머지로 학습을 하자는 것
- 과대적합과 과소적합
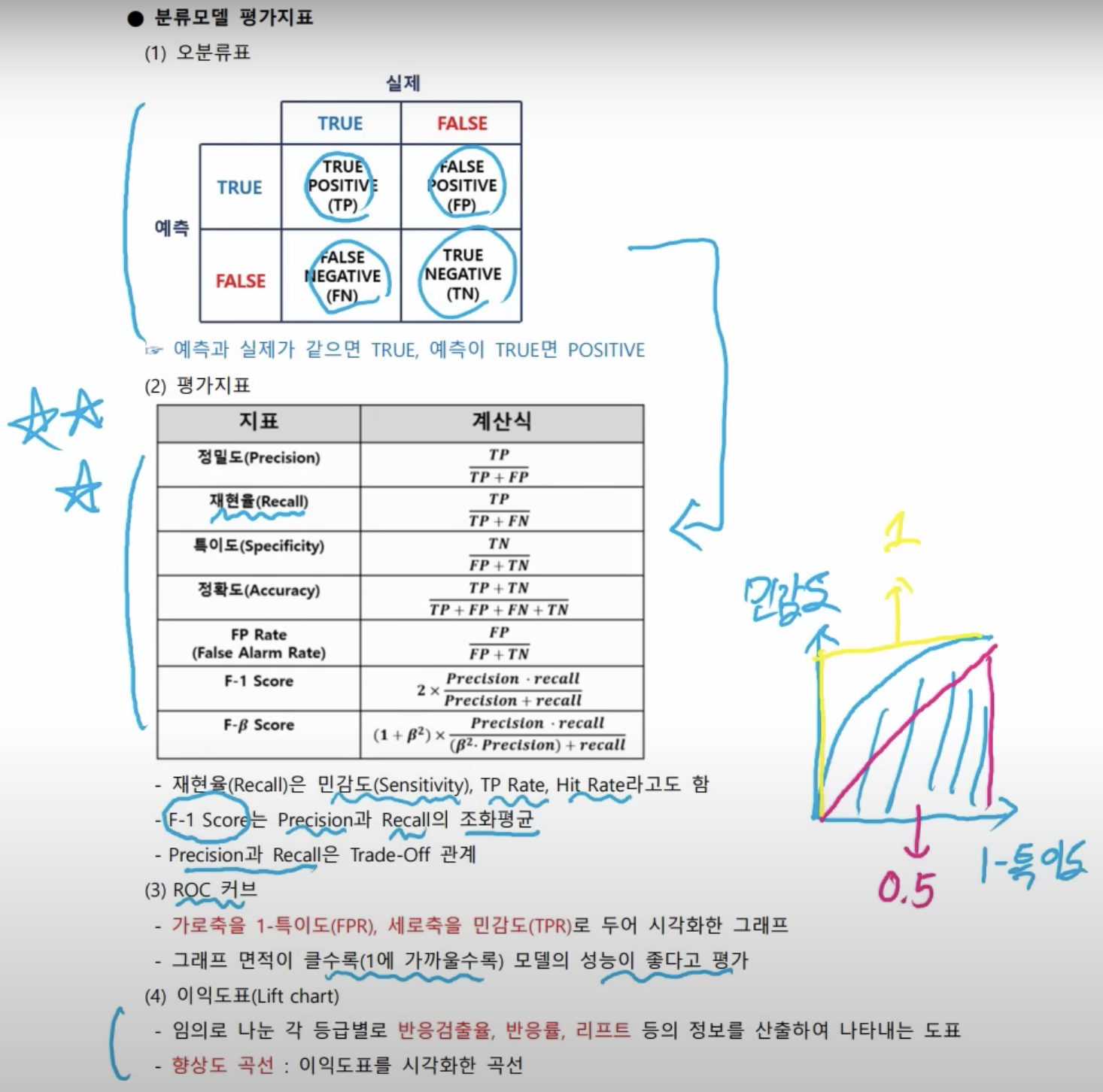
- 회귀 분석은 수치형 데이터에서 사용을 한다. 분류 분석은 범주형 데이터에서 사용한다.
- 수치형 데이터는 나이, 1,000원 2,000원 3,000원 이런 것들이고, 범주형 데이터는 0, 1(서바이브드 유무), 개냐 고양이냐 이런 것들이 범주형이다.
- 분류 분석은 범주형 데이터를 활용하는데, 분석 방법에는 로지스틱 회귀분석 의사 결정 트리 같은 방법들이 있다.
- odds는 실패할 확률 분의 성공할 확률이다. 이것을 로직변환을 취하면 양 변에 자연로그(ln)을 취한다. 기존의 회귀분석에서는 위의 선형회귀 같은 것들을 배웠었는데, 로지스틱 회귀분석은 밑에 지수(exponential, 2.7 정도의 값)가 붙은 상태로 나타난다.
- 의사결정트리는 분류에만 사용하지 않는다. 회귀에서도 사용할 수 있다. 그러나 전문적으로 분류에서 사용하므로 분류분석으로 나눠지는 것이다.
- 보팅 방법은 말 그대로 투표이다. 투표를 통해서 최종 모델을 선택하는 것이다.
- 배깅는 복원추출에 기반을 둔 붓스트랩을 생산해서 모델을 학습 후에 보팅으로 결합을 한다. 복원추출은 데이터를 넣었다 뺐다 계속하면서 데이터셋을 생성하는 것인데, 무한히 데이터를 넣었다 뺐다 해도 이 데이터가 선택되지 않을 확률은 36.8%나 된다.
- 인간의 뇌를 모방. 인간의 뇌에는 뉴런들이 연결돼 있다. 이런 뉴런들이 연결이 돼서 신호를 전달을 하면서 어떤 결과를 도출을 하는데 이것을 모방한 것이다. 하나하나를 퍼셉트론이라고 부른다.
- 퍼셉트론은 선형 회귀 모델로 되어 있다. 선형 회귀로 된 모델들을 여러 개를 결합해 봤자 선형성을 띄게 되어 있다. 선형성을 극복하기 위해서 활성화 함수를 도입을 한다.
- 회귀계수, 가중치인 w를 오차를 최소화하기 위해 회귀분석에서는 최소제곱법을 사용했다. 인공신경망에서는 경사를 내려가면서 오차가 최소가 되는 지점을 찾는다.
- 시그모이드 함수를 사용하면 너무 천천히 내려가는 가서 가중치가 갱신이 안 되기 때문에 이런 RelLU(렐루)함수 같은 걸 쓰면서 기울기 소실 문제를 극복하기도 한다.
- x
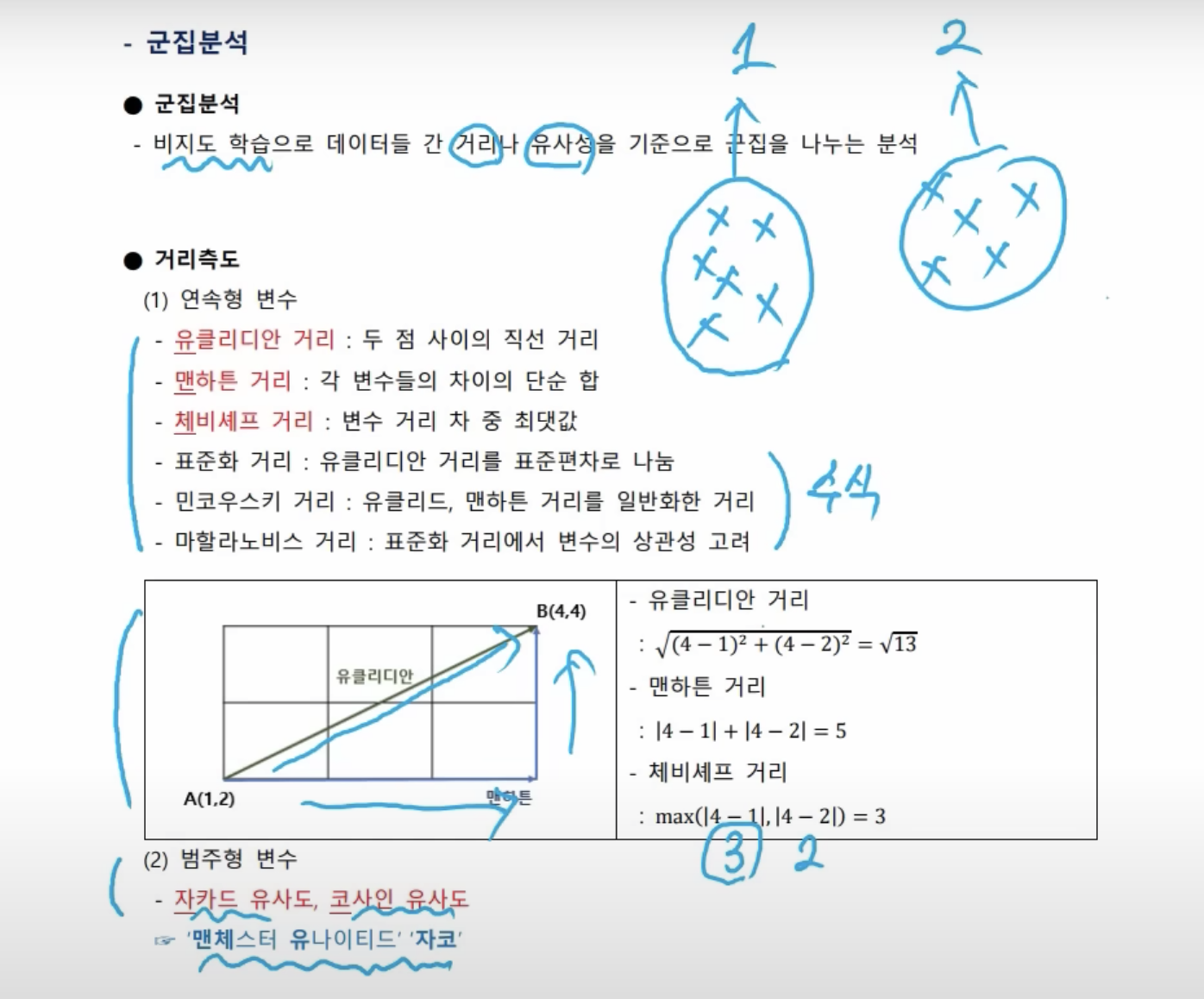
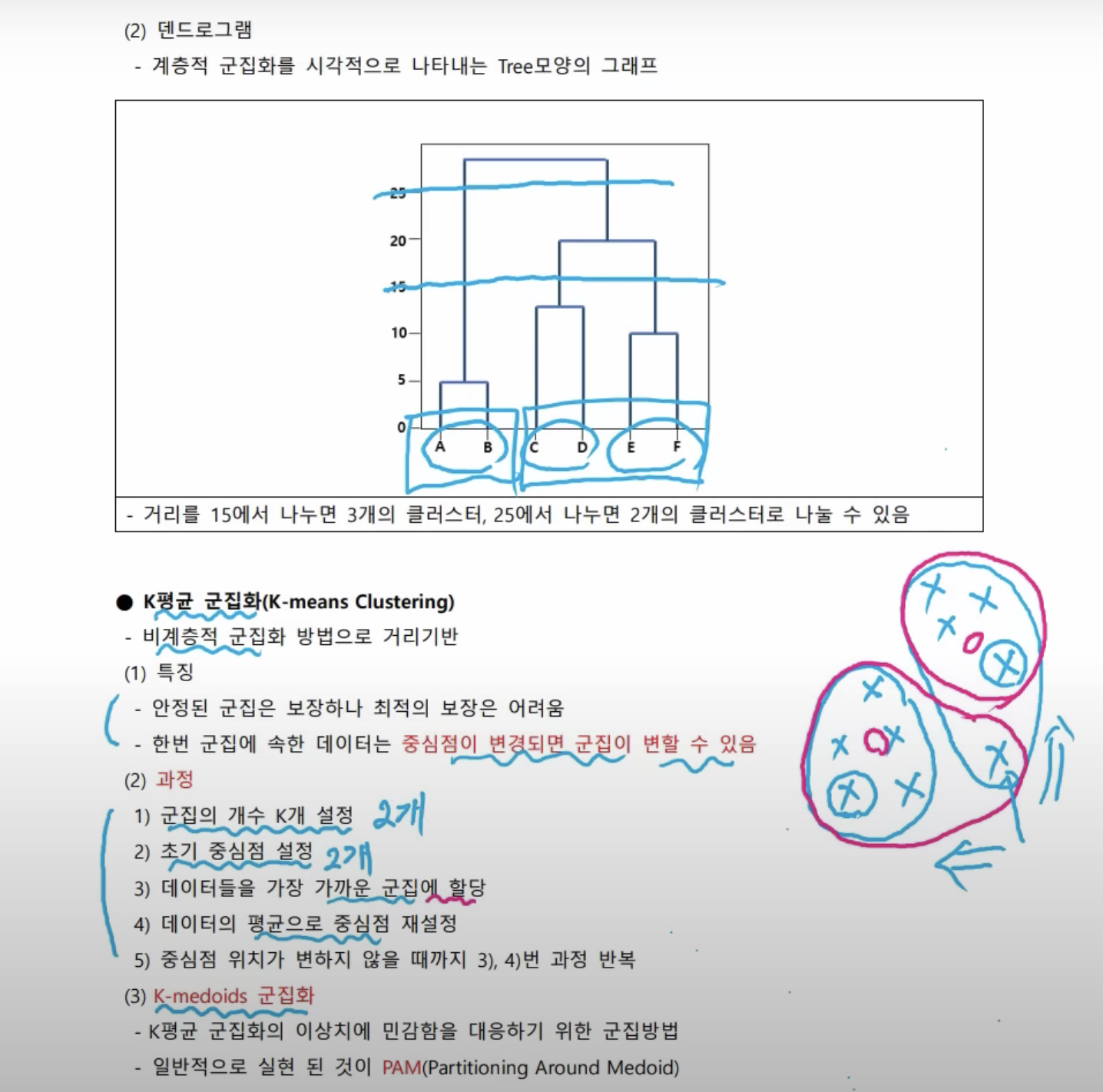
- 군집 분석은 비지도 학습이다. 즉, 정답이 없다. 분류분석에서는 강아지냐 고양이야 뭐 이런 식으로 정답이 있었지만, 군집 분석은 정답이 없어서 데이터가 거리나 유사성의 기준으로 군집을 나눈다.
- 연속형 변수와 달리, 범주형 변수는 거리를 계산할 수 없기 때문에 유사도로 계산한다.
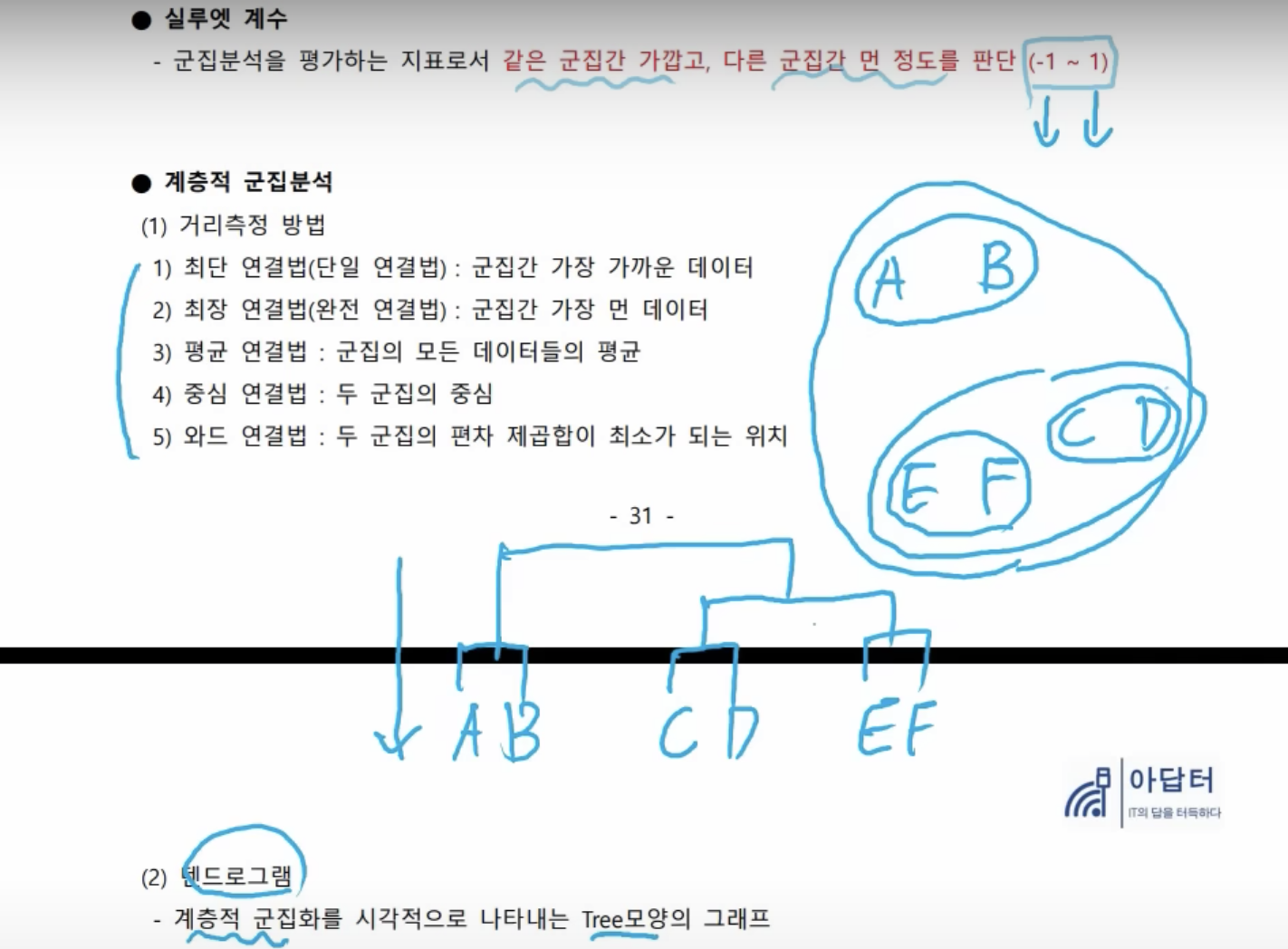
- 실루엣 계수는 같은 군집 간의 거리는 가깝고 다른 군집 간의 거리는 먼 정도를 평가한다. -1 ~1 값을 갖는데, -1이면 성능이 안 좋은 상태, 1이면 성능이 좋은 상태이다. 이걸로 군집 분석을 평가를 한다.
- 위에서는 가까운 거 위주로 묶어 줬다. 이 거리를 측정하는 방식이 다섯 가지 방식이 있다. 어떤게 어떤 방식으로 사용이 된다라는 걸 알아야 한다.
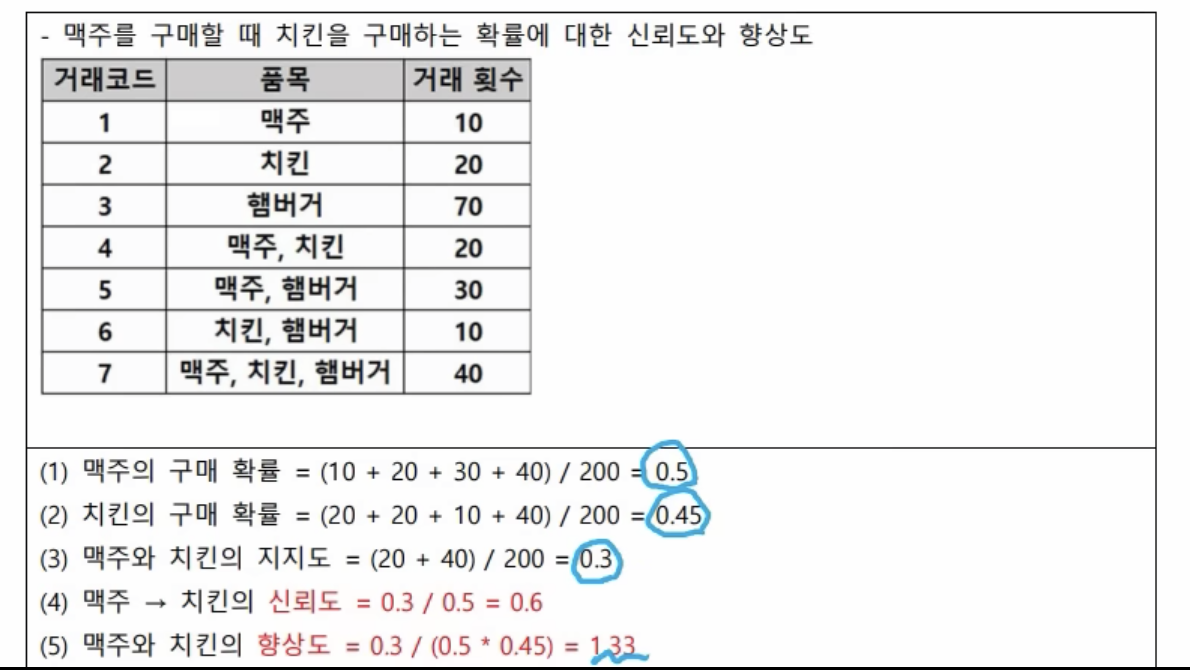
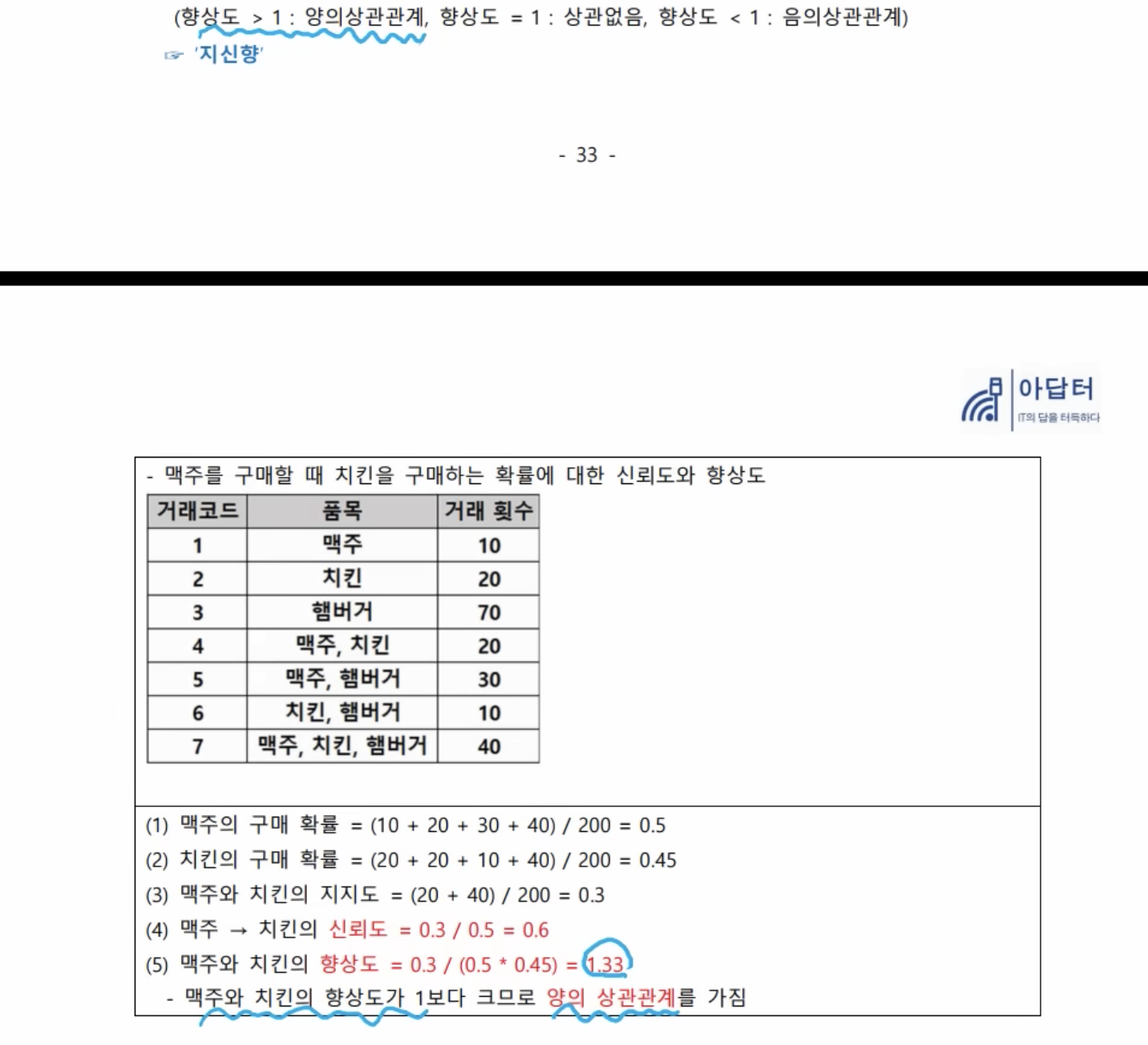
- 상관계수는 0으 판단, 향상도는 1로 판단
- 1보다 크니까 양의 상관 관계를 갖는다. 맥주를 구매하면 치킨을 구매할 확률이 높다는 것이다. 그리고 치킨을 구매할 때도 맥주로 구매할 확률이 높다라는 식으로 정리를 해 볼 수 있다.
참고 자료
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.