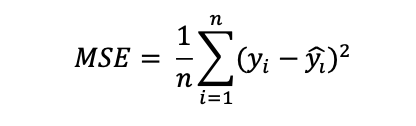40회 기출문제 분석
- 문자, 1바이트는 8비트
- 정형, 반정형, 비정형, 정량적 데이터
- 군집 분석은 예측보다는 비슷한 데이터끼리 묶는 방법
- 유전알고리즘 - 최적화, 문제 해결: 최적화를 시키는 과정에서 문제를 해결하고, 다양한 해결책을 제시하고, 더 좋은 해결책을 찾는다.
- 시각화만 나왔으면 하드스킬, 설득력이므로 소프트스킬
- 분산: 전사차원 관리. 별도의 조직으로 존재하게 된다. 각 팀에 파견을 나가서 분석업무 수행
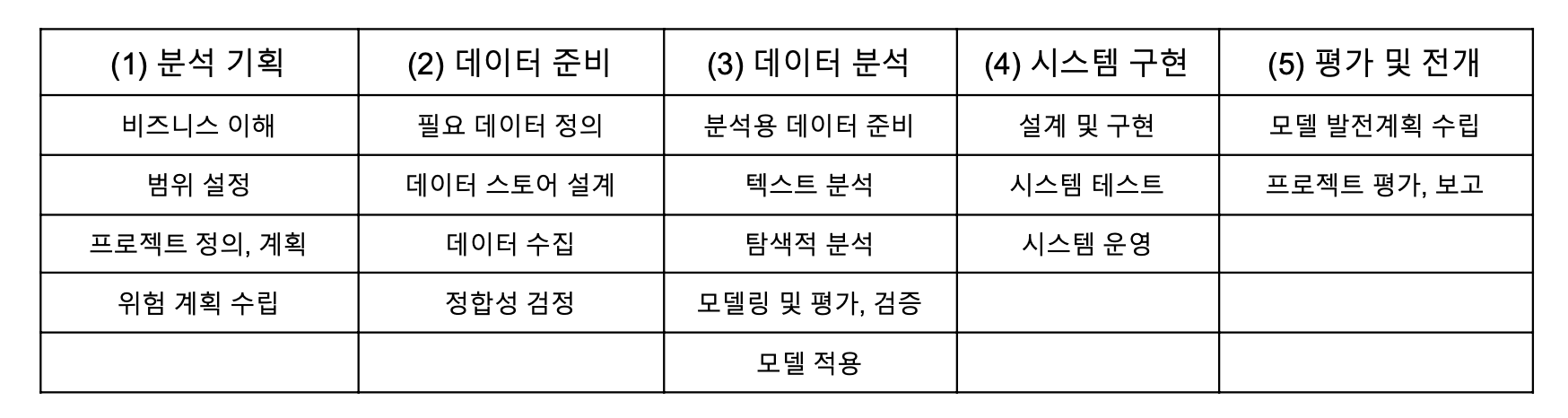
빅데이터 분석 방법론[준비, 분석, 구현, 평가 및 전개]
- 완벽한 계층적 프로세스 모델로서 단계, 태스크, 스텝의 3계층 레벨과 5단계로 구성되어 있다.
- 5개의 단계들을 프로세스 그룹이라 하며, 각 단계는 여러 개의 태스크로 구성되는데 각 태스크는 물리적 또는 논리적으로 품질 검토의 항목이 될 수 있다.
- 마지막 계층인 스텝은 입력자료, 출력 및 도구, 출력자료 등으로 구성된 단위 프로세스들이다.
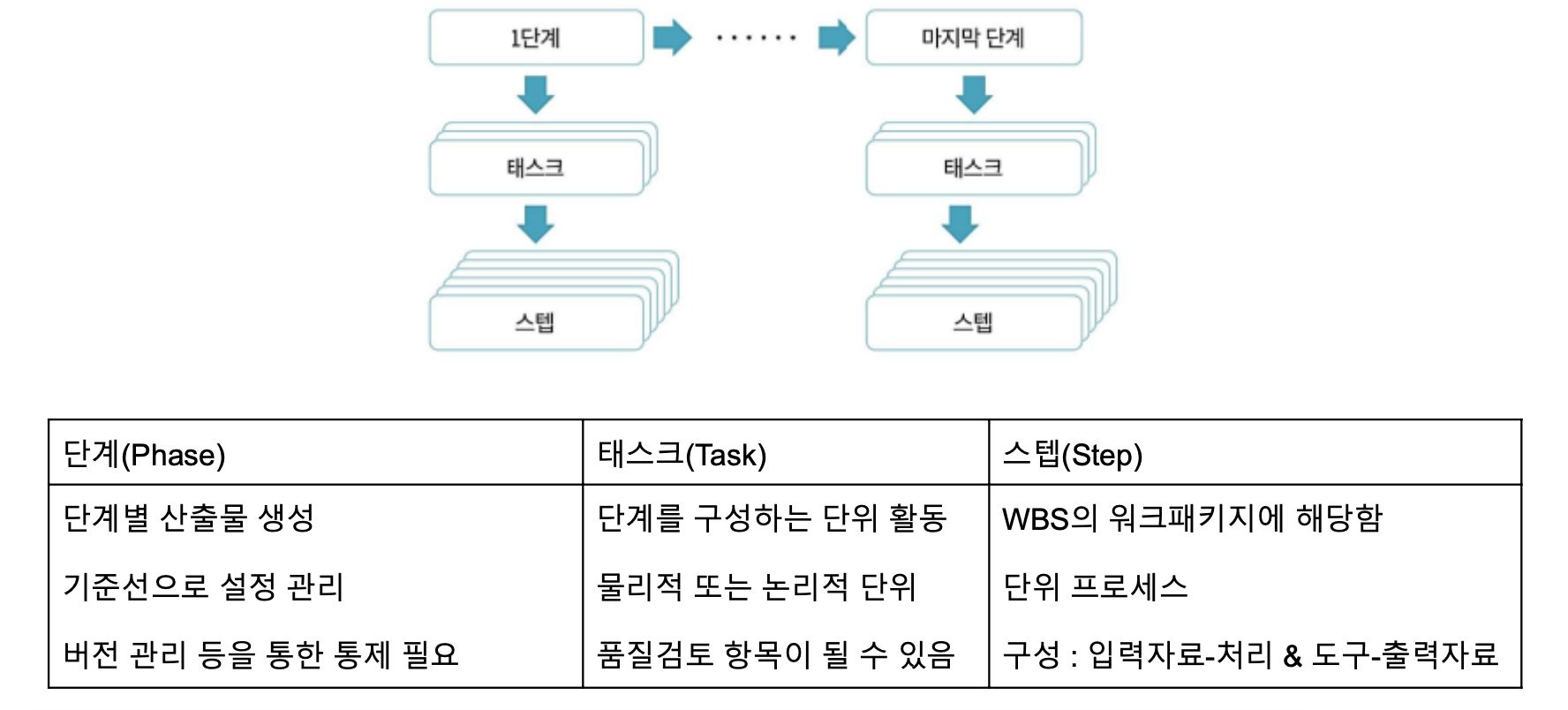
- ▶ 분석 방법론의 계층 프로세스
① 단계(Phase) [최상위 계층] : 프로세스 그룹을 통해 단계별 산출물이 생성
② 태스크(Task) [중간 계층] : 단계를 구성하는 단위 활동
③ 스텝(Step) [최하위 계층] : WBS(Work Breakdown Structure) 작업단위로 입력자료, 처리 및 도구, 출력자료 등 세부적인 단위 프로세스
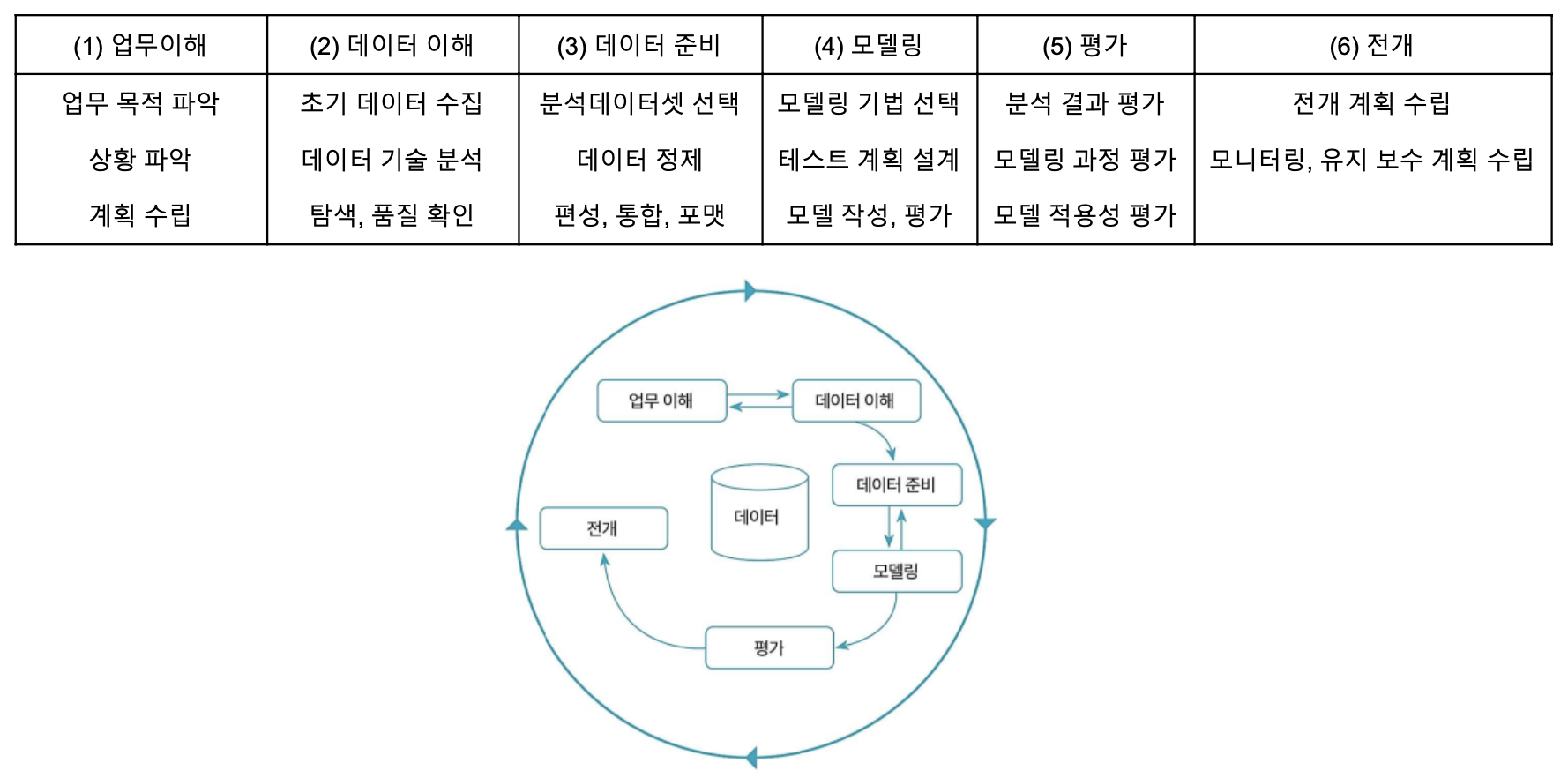
전통적인 분석 방법론 ( CRISP─DM 분석 방법론 ) [업데 준모평 전(배)]
- KDD 분석 방법론과 비슷하나, 약간 더 세분되어 있다는 점이 차이점이다.
계층적 프로세스 모델로 단계, 일반화 태스크, 세분화 태스크, 프로세스 실행의 4개의 레벨과 업무 이해, 데이터 이해, 데이터 준비, 모델링, 평가, 전개의 6단계로 구성되어있다.
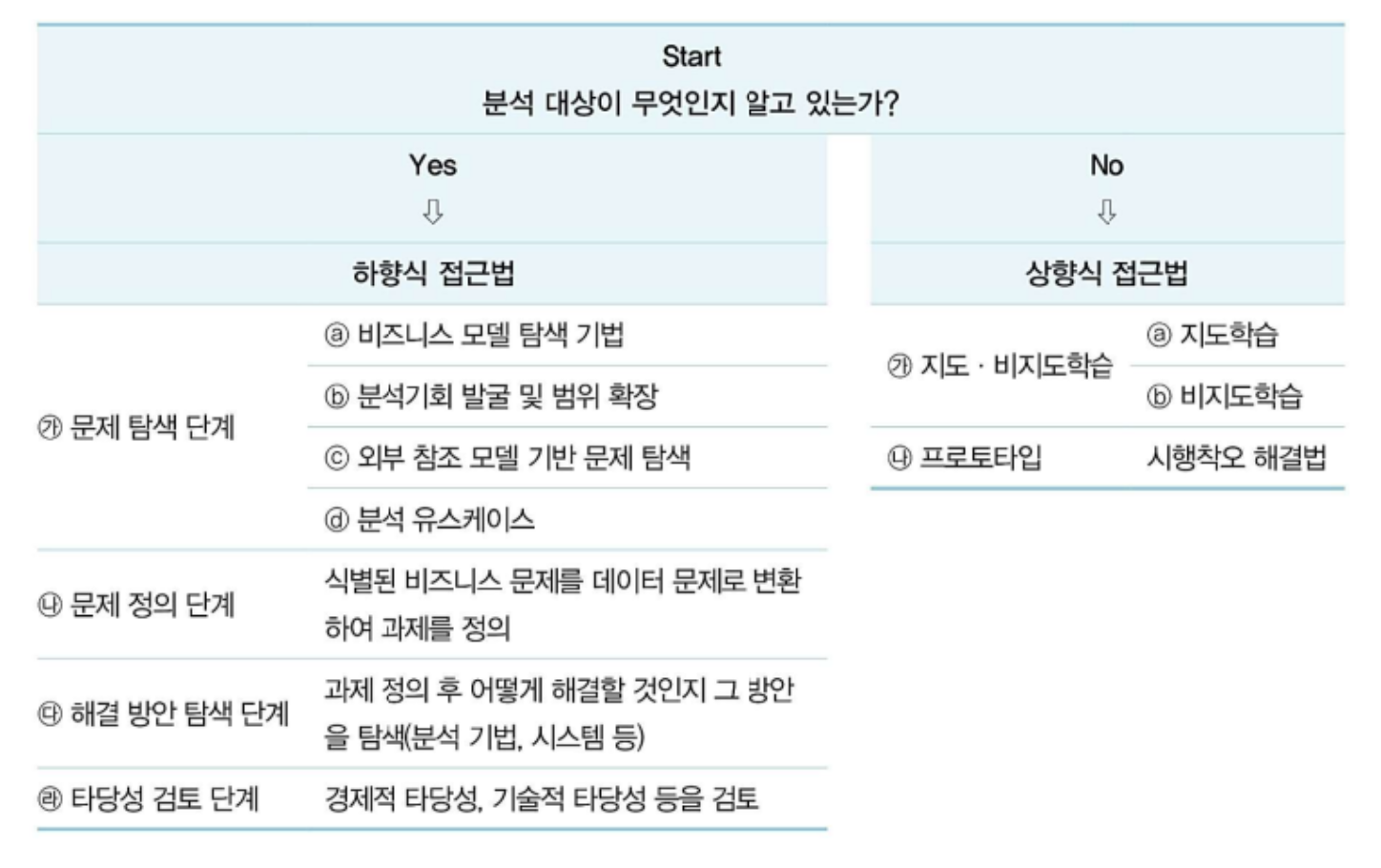
- 과제가 정의되어 있지 않기 때문에, 비슷한 과제 혹은 비슷한 주제끼리 묶을 필요가 있음 → 일반적으로 비지도 학습 수행
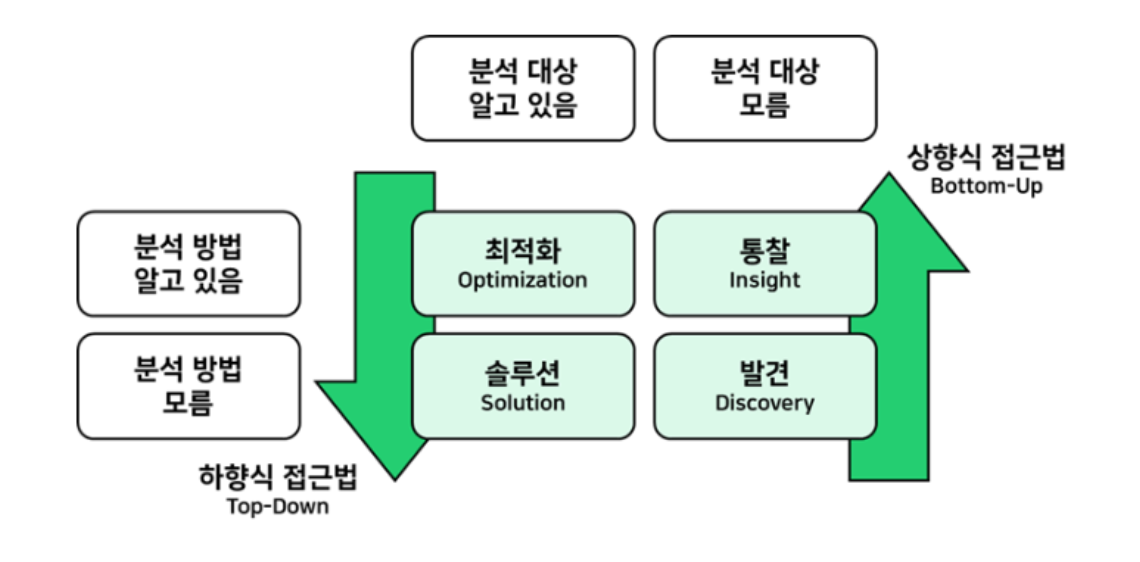
- 프로토타이핑은 상향식에 가깝다.
- 분석 과제 발굴
- 해결해야 할 다양한 기업(혹은 분석의 주체)의 문제를 ‘데이터 분석 문제’로 변환하는 것을 포함하는 개념이다.
- 분석 과제는 이해관계자들이 이해할 수 있게 프로젝트 수행 목적의 과제 정의서 형태로 도출된다
- 솔루션을 찾는 것은 하향식 접근법
분석 과제 탐색 방법
- 하향식 접근법(TOP-DOWN)
- 분석 대상이 무엇인지 알고 있음
- 문제탐색-문제정의-해결방안탐색-타당성검토
- 최적화 → 솔루션
- 상향식(BOTTOM-UP)
- 분석 대상이 무엇인지 모름 → 데이터에서 인사이트 발견
- 지도학습, 비지도학습, 프로토타입 방식
- 발견 → 통찰 (인사이트)
- 하향식 접근법(TOP-DOWN)
- 과제 접근론 방법 - 과제 중심적, 마스터 플랜 기반(롱텀 뷰)의 접근 방식
- 누적 기여도 = 전체변이 공헌도
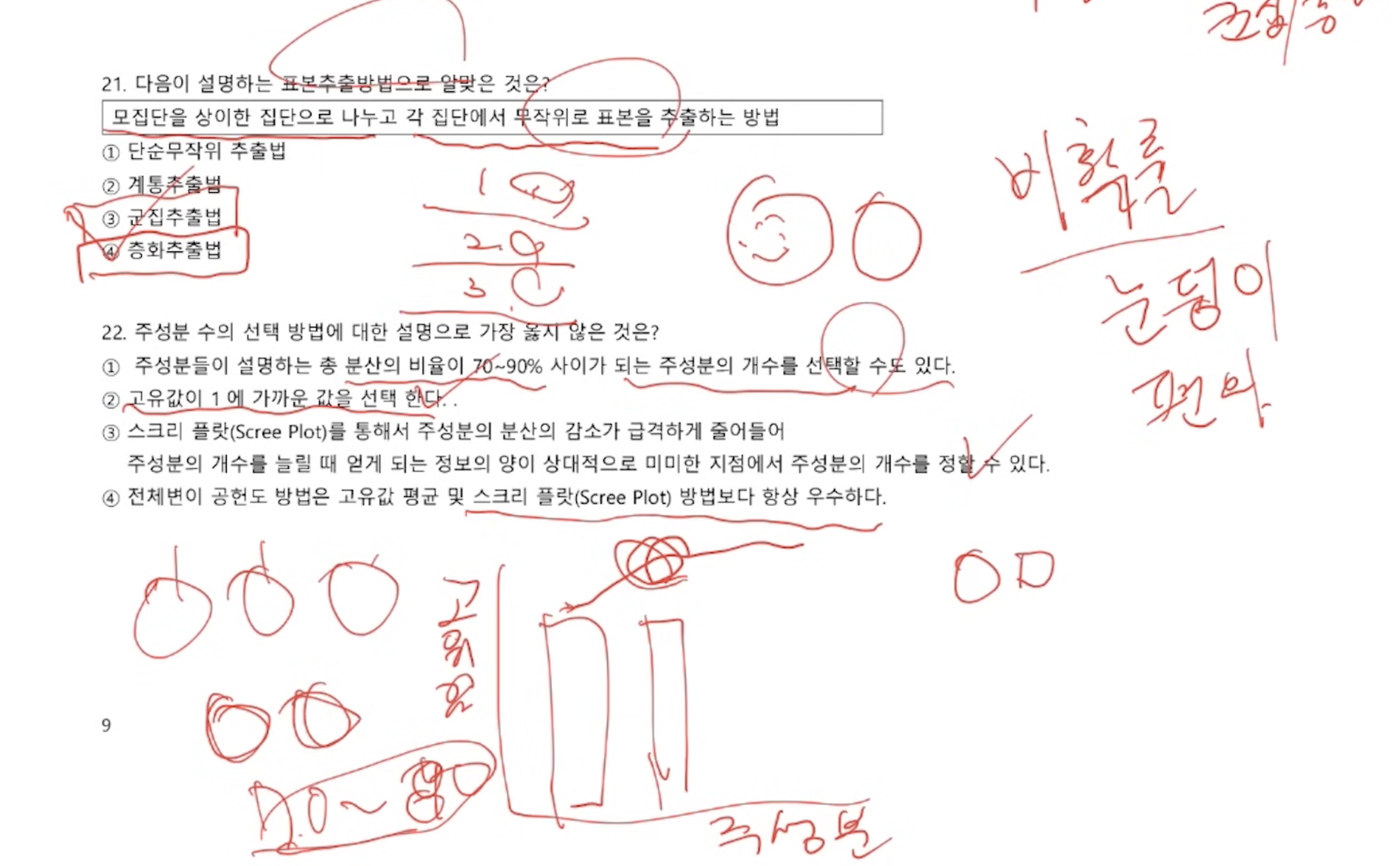
- 표본추출 방법
- 단순 랜덤 추출법 표본추출 방법 중 가장 쉽고 단순한 방법이며, N개의 모집단에서 n개의 데이터를 무작위로 추출하는 방법이다.
- 계통 추출법 모집단의 원소에 차례대로 번호를 부여한 뒤 일정한 간격을 두고 데이터를 추출하는 방법이다.
- 집락(군집) 추출법 데이터를 여러 집락으로 구분한 뒤, 단순 랜덤 추출법에 의하여 선택된 집락의 데이터를 표본으로 사용하는 방법이다. 각 집락은 서로 동질적이며, 집락 내 데이터는 서로 이질적이다.
- 층화 추출법 층화 추출법은 집락 추출법과 유사하나 반대의 성격을 지닌 추출 방법이다. 데이터를 여러 집락으로 구분하지만 각 집락은 서로 이질적이며, 군집 내 데이터들은 서로 동질적이다.
- 비례 층화 추출법은 전체 데이터의 분포를 반영하여 각 군집별 데이터를 추출하는 방법이다. 1학년 200명, 2학년 300명, 3학년 500명인 학교에서 표본을 추출한다면 2 : 3 : 5를 유지해서 표본을 추출하는 방법이다.
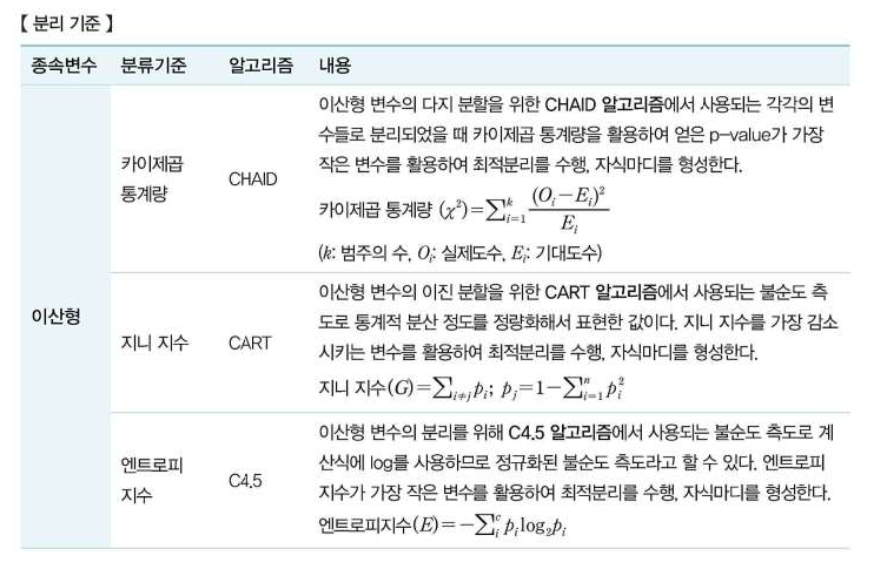
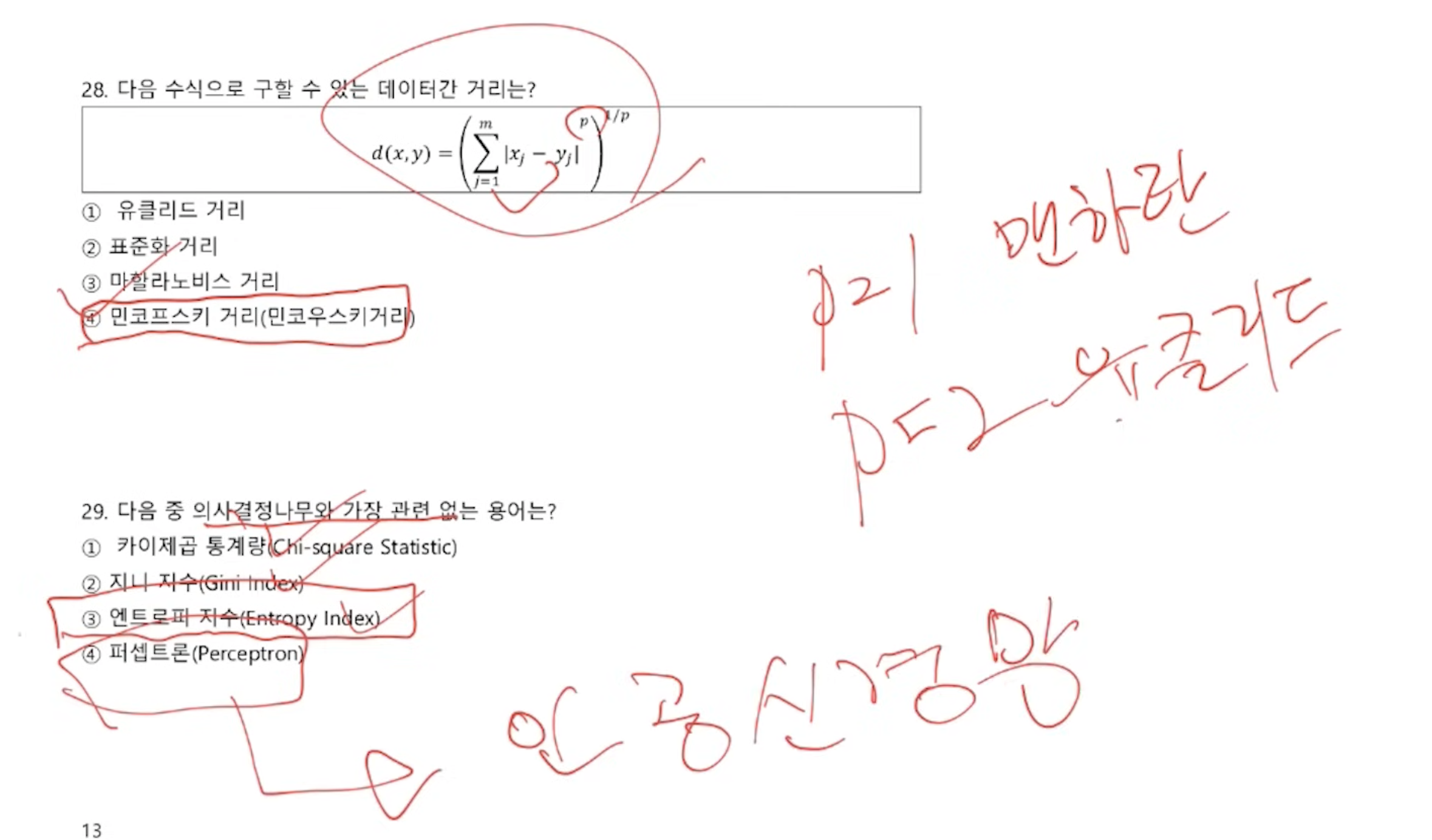
- 분류나무: 카이제곱, 엔트로피지수, 지니지수
- c는 범주의 수, p는 범주의 비율
- 엔트로피가 크면 클수록 불순도가 높다.(=이질성이 크다.) 엔트로피 값이 작은 방향으로 분리된다. 이 값은 0과 1 사이의 값으로 산출된다.
- 엔트로피 지수(E)와 지니 지수(G)
지니 지수는 불순도를 나타내는 값이므로 낮을수록 좋으며, 반대로 엔트로피 지수는 순수도를 나타내는 값이므로 높을수록 좋다.
- 엔트로피 지수(E)와 지니 지수(G)
- 독립사건이 아닌, 배반사건을 말한다.
- 종속사건: 비가 올 때 우산이 잘 팔릴 확률
- 독립사건: 비가 올 때 동전의 앞면이 나올 확률 → 각각 독립이지만, 동시에 일어날 수 있는 사건이다. A ∩ B = P(A) * P(B)
- 배반사건: 동시에 일어날 수 없는 사건을 의미한다. A ∪ B = P(A) + P(B)
- 왼쪽은 연속형이기 때문에 평균값과 중앙값이 나오고, 오른쪽은 유형별 데이터의 건수를 보여주고 있으므로 범주형 데이터이다. 달리 표현되는 형태 기억!
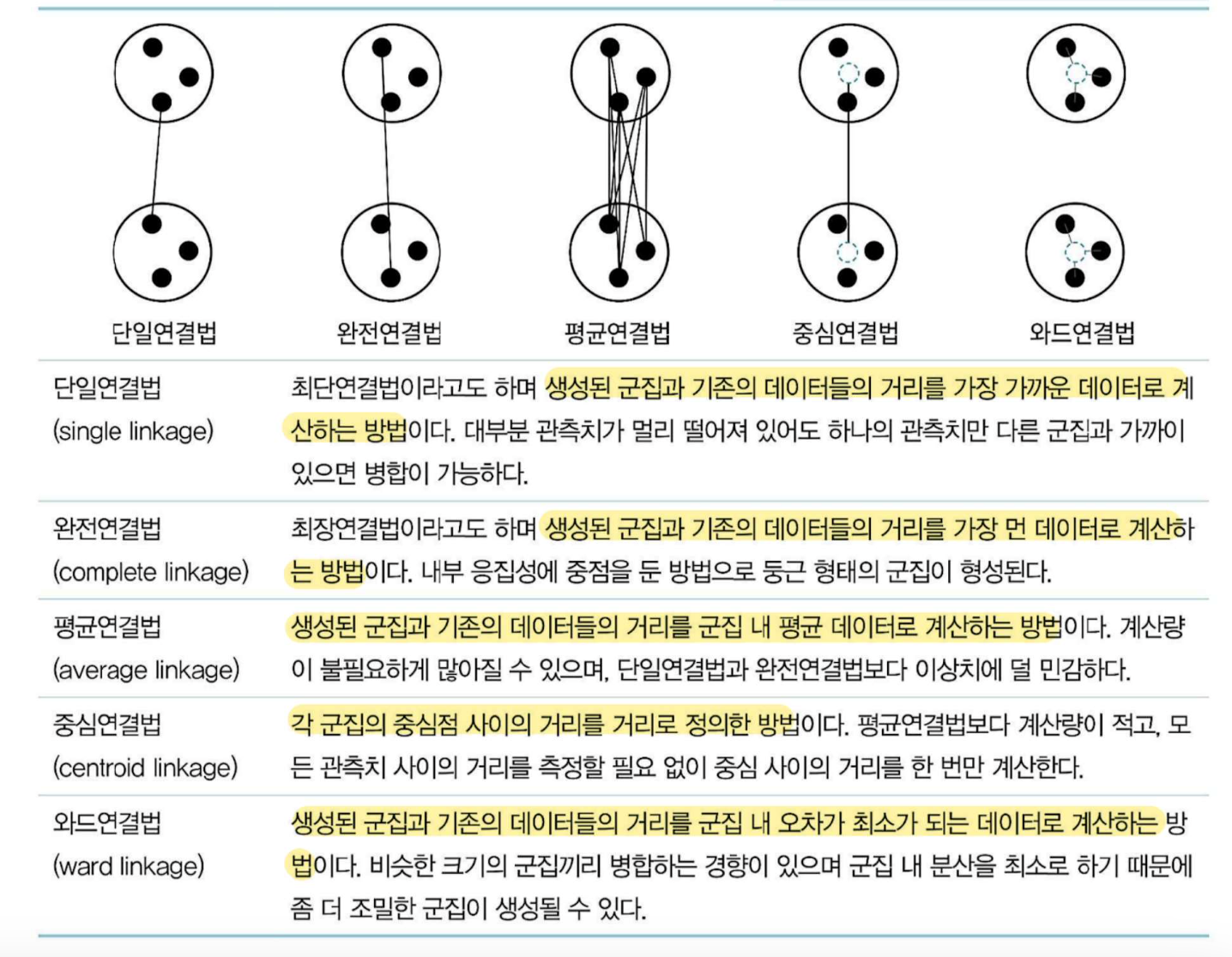
- 계층적 군집 방법은 하나의 데이터를 개체로 보고, 각각의 값을 거리를 재서 하나씩 합쳐가면서 군집을 만든다.
- 집단과 집단 사이의 개체에 대해서 어떤 값을 기준으로 측정할 것인가
- 계층적 군집분석
- 개별 관측치 간의 거리를 계산해서 가장 가까운 관측치부터 결합해나가면서 계층적 트리 구조를 형성하고, 이를 통해 군집화를 수행하는 방법이다.
- 병합적 방법 전체 데이터를 하나의 군집으로 간주하고 가까운 데이터부터 순차적으로 병합한다
- 분할적 방법 전체 데이터를 하나의 군집으로 간주하고 각각의 관측치가 하나의 군집이 될 때까지 군집을 순차적으로 분할한다.
군집 간의 거리 측정 방법
- ▶ 와드연결법: 군집내의 오차제곱합에 기초하여 군집 형성
- 개별 관측치 간의 거리를 계산해서 가장 가까운 관측치부터 결합해나가면서 계층적 트리 구조를 형성하고, 이를 통해 군집화를 수행하는 방법이다.
- 분해시계열: 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법 ⤷경향(추세)요인, 계절요인, 순환요인, 불규칙요인으로 이루어짐
- 경향은 말 그대로 자료가 오르거나 내리는 추세를 의미 계절은 고정된 주기에 따라 자료가 변하는 경우 순환은 경제적이나 자연적인 이유 없이 알려지지 않은 주기를 갖고 변화 불규칙은 위 3가지로 설명할 수 없을 때
맨하튼, 유클리디안, 민코우스키
- 정해져있는 값의 범위가 없다. → 표준화시켜 만든 것이 상관계수
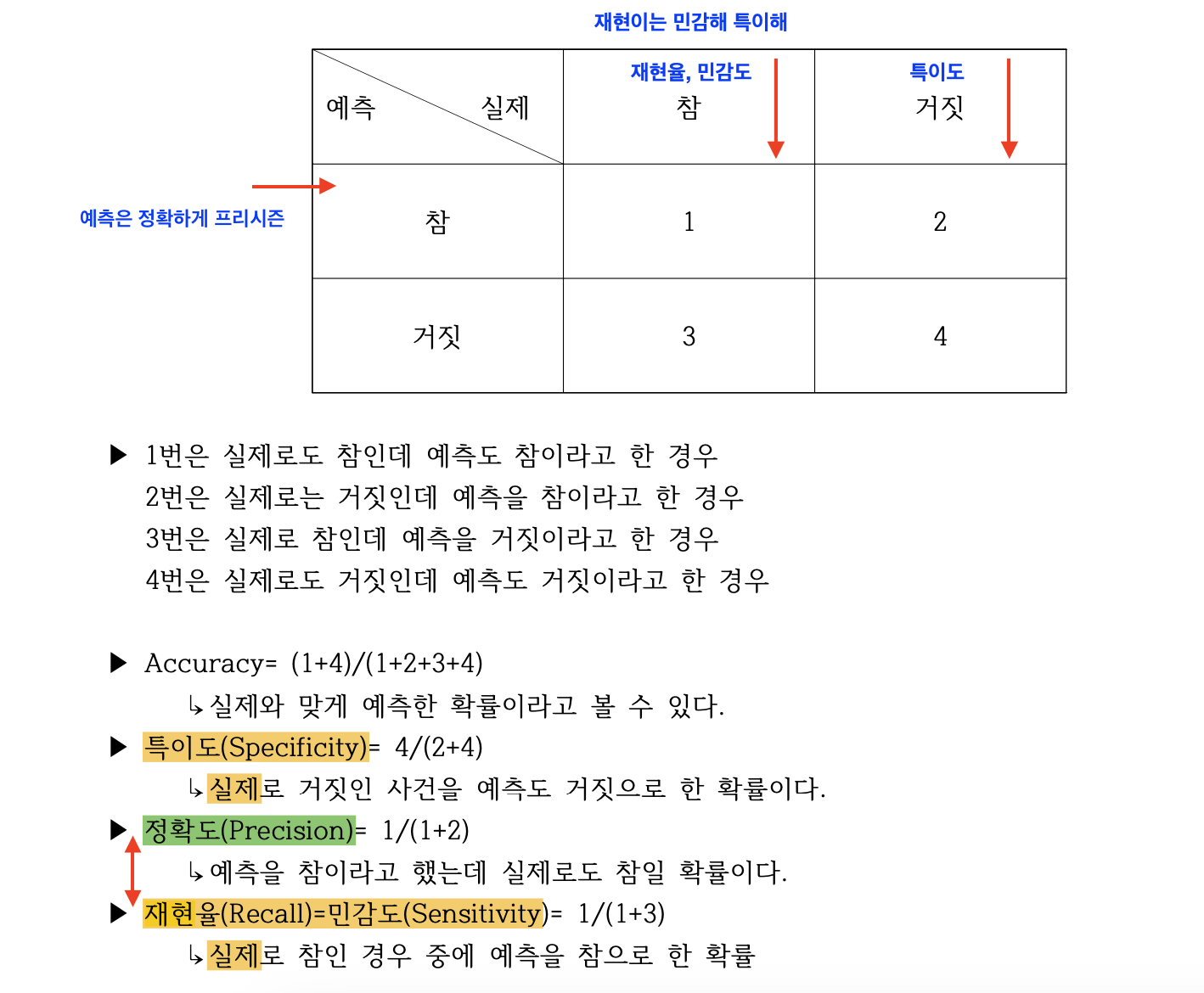
- F1 score는 분류모델을 평가하는 지표
- 베타를 매개변수로 재현율과 정확도 평균가중치를 부여해서 평가
- 1보다 크면 재현율(recall)에 가중치를 두고, 1보다 작으면 정확도(precision)에 가중치를 둔다.
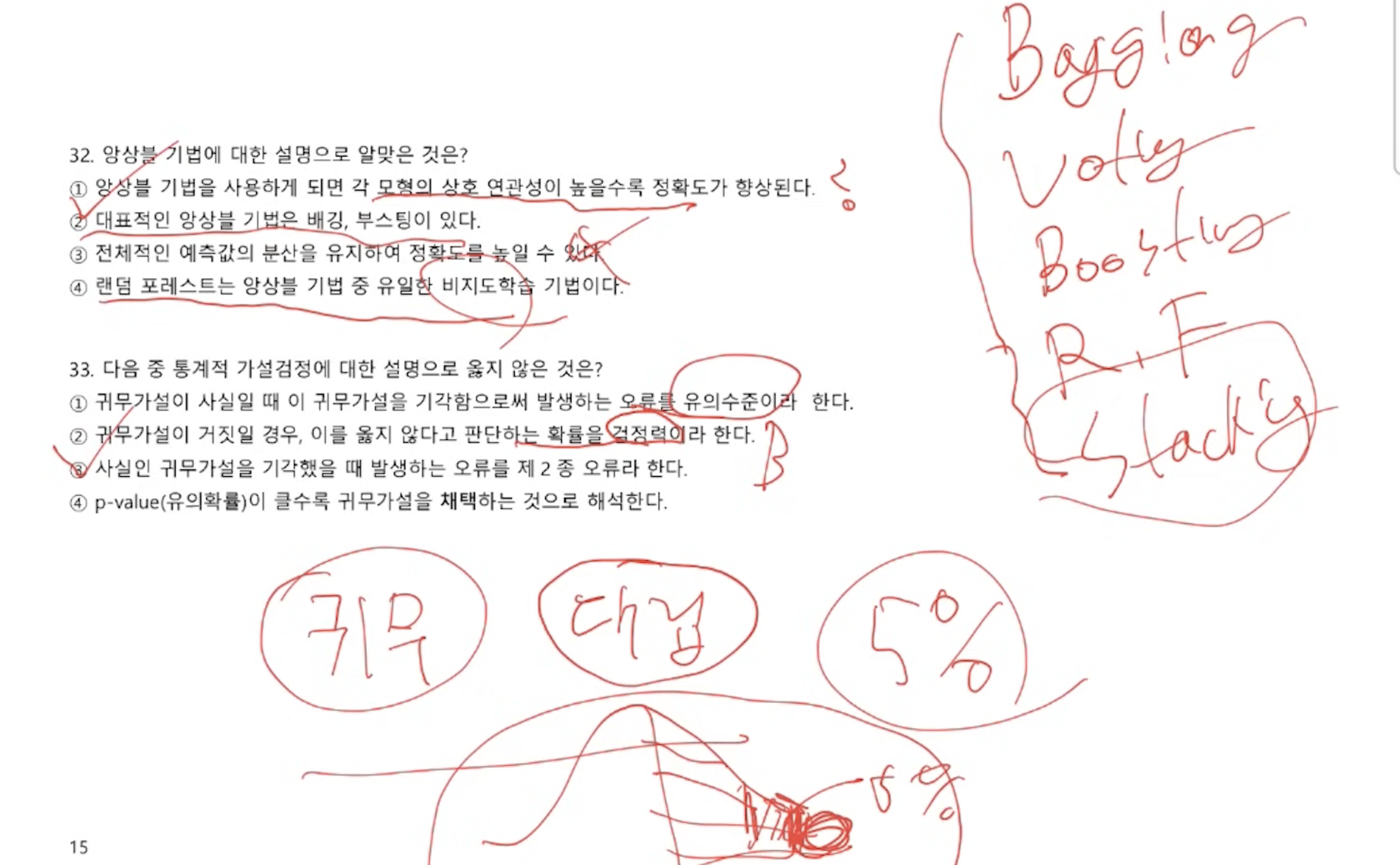
- 모형의 상호연관성이 아닌 데이터의 다양성이 맞다. 모델을 다양하게 하는 방법이 스태킹(stacking)
- 분산을 유지하는 것은 데이터의 다양성으로 이어질 수 있으나, 그 대표성을 표현한다는 의미가 더 맞다.
- 랜덤 포레스트는 지도학습
- 통계적 가설검정은 우리가 주장하고자 하는 가정(대립가설)을 기사실과의 관계(귀무가설)를 가지고 증명하는 방법을 가설검정이라고 한다.
- 유의수준은 보통 5%이다.
- 귀무가설이 거짓일 경우, 이를 옳지 않다고 판단하는 확률을 검정력 베타라고 한다.
- k-means는 특정 위치를 옮겨다니면서 평균을 측정하고, 그 값이 감소하지 않는 시점에서 군집을 확정하는 매커니즘을 따른다.
- 비지도학습, 군집분석, 비계층적 군집(미리 k값을 군집 수로 알려주는 알고리즘)
- k-means는 노이즈에 약하기 때문에, 노이즈에 약한 단점을 적용한 것이 k-medois 알고리즘이다.
초승달 모양은 DBSCAN - 밀도기반의 군집
- 오차 = 모집단의 데이터를 활용하여 회귀 식을 구한 경우 예측값 - 실제 값의 차이
- 잔차 = 모집단을 대표하는 표본집단의 데이터를 활용하여 회귀 식을 구한 경우 예측값 - 실제값이 차이
MSE(Mean Squared Error) : 실제 값과 예측 값의 오차 제곱합을 평균 계산한 것으로, 평균 제곱 오차라고 한다.
참고 자료
- https://www.youtube.com/watch?app=desktop&v=RWHi3lGgiHA
- https://www.youtube.com/watch?v=xJ04s8KxGGI
- 전용문, 박현민 저자.2024 이지패스 ADsP 데이터분석 준전문가.위키북스.2024년 01월 12일
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.